1954 Geometria 024

6.    Obr. 37. Krużnice lc_v k₂ maju yonkajśi dotyk v bodę T, priamka A₁A₂ sa dotyka obidvoch krużnic v bodoeh A_x, A₂, spolocna dotyć-nica v bodę T pretina priamku A₁A₂ v bodę Q. Dokażte, że uhly

S₁QS₂ a A^TA₂ su prave (S_x, S₂ su stredy krużnic k_v Jc₂).

7.    Na obr. 38 je S stred krużnice, <£ ASB = 36°, <f_ ASO = 60°, <£ ASD = 150°.

a)    Urćte AFB, F BFC, < AEI), <£ CED.-

b)    Urcte \ DAF, ak je ASF = 2 <£ DSF.

8.    Urcte uhly trojuholnika, który dostanete, ak spojite na ciferniku hodin cislice 2, 6, 9.

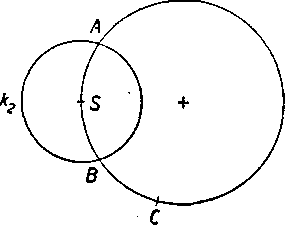
Obr. 40

9. Dve tetiyy AB, CD sa preti-naj u kolmo vo ynutri krużnice. Ak je BAC = 45°, urcte <£ABD.

10.    Na obr. 39 je AB SD roynobeż-nik. Urcte uhol w.

11.    Obr. 40. Stred S krużnice k₂ leżi na krużnici k_v Dokażte, że polpriamka CS je os uhla <£ ACB. Pritom C je 1’uboyol-ny bod toho obluka AB, na ktorom nełeżi stred S.

12.    Dve krużnice sa pretnu vo dvocb bodoeh A, B. Ak su AC, AD priemery krużnic, leżia body B, C, Dy priamke; dokażte to.

13.    Dokażte, że v śtvoruholniku, któremu możno opisat krużnicu, je sucet każdych dyoch protilahlych uhlov uhol priamy. Możno tuto vetu obratif?

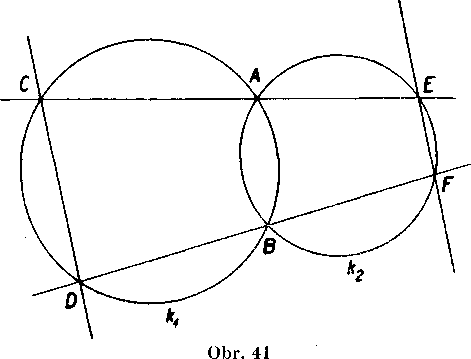
14. Krużnice k_v k₂ sai, pretinaju vo dvoch bodoeh A, B. Nimi yedieme podia obr. 41 sećny CAE a DBF. Dokażte, że je CD || EF. Navod: Vyjadrite uhly śtyoruholnika CDFE pomocou uhlov CAB a <£ DBA.

5. Konstrukcne ulohy

V 7. i v 8. rocniku sme rieśili mnoho konstrukcnych ul oh. Pritom sme zachovavali urcity postup, który zarućuje, że uloha budę spravne a celkom rozrieśena.

Najskór sme urobili (pomocou nacrtku) rozbor ulohy. Pri rozbore predpokladame, że uloha je rozrieśena (t. j. je rieśitelna) a Madame yzfah medzi danymi prvkami a utyarom, który mamę zostrojit.

Z rozboru vyplynie konstrukcia ulohy, t. j. postup zostrojenia hla-daneho utvaru. Musime vśak urobifi dokaż konstrukcie; za tymto uce-lom spravidla obratime postup, który sme poużili pri rozbore.

Nakoniec urobime diskusiu ulohy. To znamena, że skumanie, ci je uloha rieśitelna vżdy, alebo len za urcitych podmienok, a kolko ma rieseni.

Prildad 3. Su dane dve róznobeżky p, q a dve kladne cisla d, r. Mamę zostrojit kruźnicu o polomere r tak, aby sa dotykała priamky p a aby \^ryt'a!ti na priamke q tetivu dlżky d.

Riesenie. a) Rozhor. Obr. 42. Pretoże je polomer dany, treba urcit stred krużnice.' Stredy Ysetkych krużnic o polomere r, które sa dotykaj u priamky p, vyplnia dve priamky p₁. p₂, rovnobeżne s priamkou p, vedene vo vzdialenosti r. Na niektórej z priamok p_v p» leżi bladany stred S.

Stredy vśetkych krużnic o polomere r, które yytinaju na priamke q tetivu dlżky d, vyplnia oplif dve rovnobeżky q_v q₂ s priamkou q. Ich vzdialenost od priamky q je bud dlżka odvesny pravouhleho trojuhol-

d

2

a preponu r, bud je nula,

nika, ktoreho druha odvesna ma dlżku

ak je r = —. Na niektórej z priamok q_v q₂ leżi hladany stred S.

b) Konstrukcia a jej dSkaz. Zostrojime priamky p_v p₂, q₁. q₂ a najde-^rr|e spolocny bod niektórej z priamok p_lt p₂ s niektorou z priamok q_v q₂.

25