1954 Geometria 018

Teraz doplnime doterajśie poznatky o krużnići ylastnosfami obvo-doveho uhla.

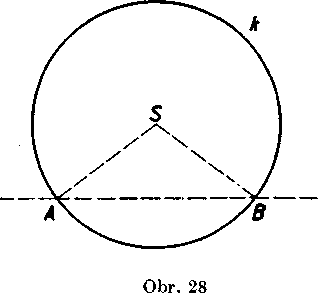
Na obr. 28 je kruźnica k = (S; r) a na nej dva różne body A, B. Body A, B delia krużnicu k na dva obluky. Ak je tetiva AB priemer,

Obr. 29

su obidva uhly A SB priame, obidva obluky su zhodne a nazyvaju sa polkrużnice. Ak je tetiva AB mensia neż priemer, je jeden z uhlov ASB duty, druhy yypukly. Obluk leżiaci v dutom uhle ASB budeme vola£ mens! obluk AB, obluk leżiaci vo vypuklom uhle ASB budeme yolat

vać§l obluk AB. Uhol ASB (ci uż duty, priamy alebo vypukly), v kto-rom leżi obliik, vola sa stredoyy uliol prlslusny k obluku.

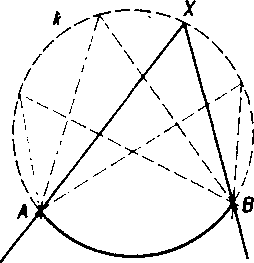
Na obr. 29 je vyznaeeny obluk AB krużnice k a bod X tej to krużnice, który obluku neprislucha. Duty uhol ■i' AXB sa nazyva obvodovy uhol, prlsluSny k obluku AB. K obluku prislucha nekonećne mnoho obvodo-vych uhlov (pozri obr. 29). Plati vśak veta:

(8) YSetky obvodove uhly prislusne tomu istemu obluku su navzajom zhodne a su zhodne s polovicou prlslusneho stredoveho uhla.

Vetu (8) dokażeme v troch ćastiach.

1. Najpry dokażeme; Ak je <£ AXB obvodovy uhol, prlsluSny k ob-

luku AB a <£ AYB obvodovy uhol (na tej istej krnżnici) prlslusny k zvysnemu obluku AB, potom suect

AXB + <£ AYB

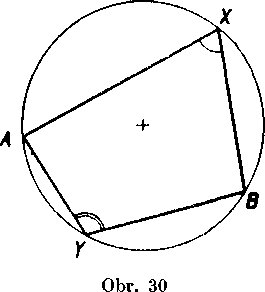
je uhol priamy (obr. 30).

X

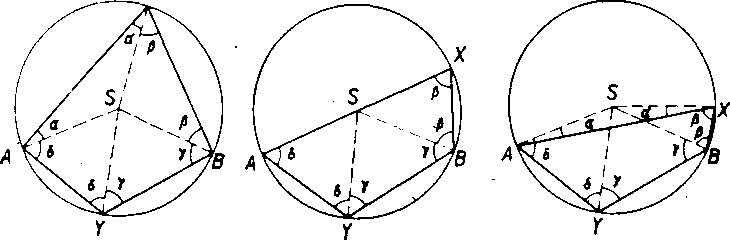
Obr. 31a    Obr. 31b    Obr. 31c

Dokaż: Body A, X, B, Y su vrcholy śtvoruholnika. Stred 8 krużnice może mat vzhIadom na tento stvoruholnik trojaku polohu: alebo leżi vo vnutri śtvoruholnika (obr. 31a), alebo na jeho obvode (obr. 31b), alebo zvonku stvoruholnika (obr. 31e). Vo vśetkych troch pripadoch su zostrojene usecky .4$, XS, BS, Y8 a v rovnoramennych trojuhol-nikoch su rovnakymi pismenami oznacene uhly navzajom zhodne.

V    prvom pripade je

c)' AXB =«-}-/?,    A YB — y -f- <5,

a dalej

<X4F=* + <5,    ^XBY=p + y.

Je teda

<£ AXB + <£AYB= -ŹXAY + XBY;

pretoże sućet vsetkych uhlov śtvoruholnika AXBY je 4R, je

AXB + <£ AYB = 2R,

co sme chceli dokazaf.

V    druhom pripade je

^AXB = fi,    <ŻAYB = y + d,

<£ XA Y = d,    XBY = p + y,

19