1954 Geometria 196

Teraz chceme zayiest pojem zhodnosti aj pre priestorove utvary. Obdobneako v rovine, axiómu zhodnosti móżeme formuloyat y prie-store. Domyslite si asi, że zyolime v priestore dve roviny q a q', v nich priamky p a p' a na priamkach p, p' body A a A'. Teraz poźa-dujeme, aby existovalo take , ,premiestenie“ priestoru, że splynu nie-len body A a A', ale i polpriamky, polroviny a polpriestory, które su v obidyoch pripadoch oddelene.

No taketo premiestenie priestoru nie je vżdy możne. Nazornejśie neż na geometrickych utvaroch presvedcite sa o tom na velmi zna-mych predmetoch vo svojom okoli. Prayu i iavu topanku — i ked patria do jedneho paru a sme ochotni ich prehlasit za zhodne — ne-móżeme stotożnit nijakym premiesfovanim. To iste plati aj o pravej a Iavej rukayici, aj o pravej a Iavej ruke. Na rovnaku nemoż-nosf by sme narazili i pri niektórych geometrickych utvaroch, które vsak aj napriek tomu chceme povażovat za zhodne.

Zalożime teda pojem zhodnosti v priestore inak. Najprv yyrieśime jeden priklad z planimetrie.

Priklad 9. Nech su £\ABC ~ A^4'J5'C'dva zhodne trójuholniky v rovine. Vżdy możno najyiac troma osovymi sumernostami urobe-nymi za sebou zobrazit trojuholnik ABC do trojuholnika A'B'C'. Dokażte toto tvrdenie a najdite osi zmienenych sumernosti.

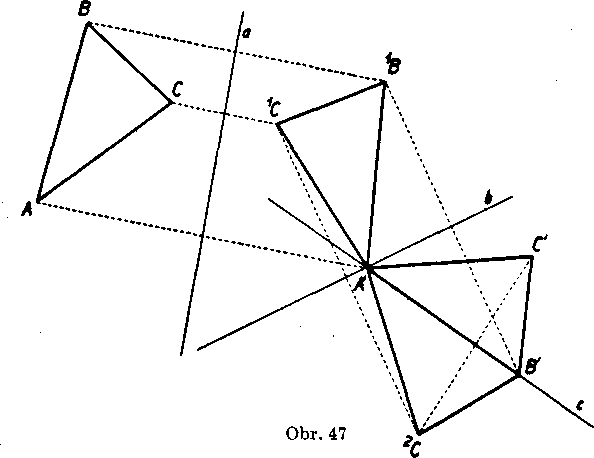
Riesenie (obr. 47). Móżeme predpokladat, że obidva trojuholniky nie su totożne, a że teda napr. A $ A'. Za os prvej osovej sumer-nosti zvoIme priamku a, która je osou usećky AA'. V tejto sumernosti je obrazom bodu A bod A’, bodu B urcity bod ¹B a bodu G urcity bod ¹C, które vieme zostrojif. Pretoże v osovej sumernosti plati

AB — A TB; AC = A’¹C\ BC = ¹B^lC,

marne

ABC^ĄA^BW (sss).

Ak su trojuholniky A'^XB^XC a A'B'C' totożne, riesenie naśho prikladu sme skoncili a staćila jedina osova sumernost na prevedenie trojuhol-nika ABC na AA'B'C'.

Ak sa vsak trojuholniky nebudu kryt, móżeme predpokladafi, że ¹B B'. Nazveme b os usecky ¹BB'. Pretoże je A'^XB = A'B', prechadza priamka b bodom A'. V osovej sumernosti s osou b je teda bod A’ samodrużny a bodu ¹B odpoveda bod B'. Oznacime -G obraz bodu ¹C. Znovu zistime

AAWC A AA'B'*C (sss),

t. j.

AABC^ AA'R'²Ca AA'B’C'.

Posledne dva zhodne trojuholniky maju spolocne vrcholy A', B', t. j. stranu A'B', a su teda możne iba dva pripady: bud’ ²C = C' a tu je naśa uloha rozriesena; stacili len dve osove sumernosti urobene po sebe, bud body ²G a G' su sumerne zdrużene podia osi c = A'B'. V tomto pripade sumernost podia osie prevedie body A', B', ² (7 po poriadku do bodov A', B', C'. Riesenie prikladu je skoncene.

Je zrejme, że dva trojuholniky, z których jeden możno previesf do druheho urcitym poetom osovych sumernosti prevedenych po sebe, su zhodne; móżeme teda vys!ovi£ vetu:

Dva trojuholniky v rovine q su zhodne, ak jeden z nich możno pre-viesf v druhy konecnym poetom osovych sumernosti a obratene. Co plati o trojuholnikoch, możno povedat aj o IubovoInych utvaroch v royine. Nebudeme to v§ak podrobnejsie rozvadzat. Stade vyplyva nova veta o zhodnosti v rovine:

Dva utvary v rovine su zhodne, ak mdźeme jeden z nich previcsf v druhy koneSnym poetom osovych sumernosti a obratene.

Tato veta nas vedie k vysloveniu definicie zhodnych utvarov v priestore:

197