1954 Geometria 168

vety zhodnosti pre dva trojuholniky leżiace v różnych rovinach. Vy-slovime na ukażku vetn sss, ktorń v dalsom ponźijeme.

Nech je dany v rovine q trojuholnik ABC a v rovine a trojuholnik A'B'C' a nech pre ne plati AB = A’B', BC = B'C', CA = CA'. Potom su trojuholniky ABC, A'B'C' zhodne, ćo znaći: rovinu q możno premiestit tak, że bod A prejde do bodu A’, bod B do bodu B' a bod C do bodu C’.

Zhodnost obidvoch trojuholnikov zapisujeme v tom to pripade tak ako v planimetrii

A ABC A A A'B'C' (sss).

V planimetrii boi jednym zo zakladnych pojmov, opierajucich sa o zhodnost, pojem kolmych priamok. Aj v stereometrii zacneme sku-manim kolmych priamok. Naj skór odvodime dóleżitu vetu.

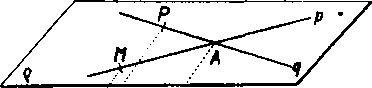
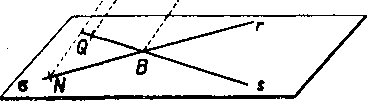
Obr. 24

Veta 12. Oznacme <£ pą jeden z ostrych ałebo prayych uhlov dvoch róznobeźiek p a q. Podobne nech <5; rs znalff jeden z ostrych alebo prayych uhlov inych dyoch róznobeźiek r a s. Ak je r || p a s || q, sii uhly *ŚC pq a rs zhodne.

Dókaz (obr. 24). Oznacme q = pq, a = rs. Podia kriteria rovno-beżnosti dvoch rovin je g \ \ a.

Vetu dokażeme najskór v pripade, że g ^ er.

Oznacme A priesecikpriamok p,q& Bpriesećikpriamok r, s. ZvoIme na priamke q bod P $ A a na priamke p bod M ♦ A tak, aby <£ MAP boi jeden z ostrych alebo pravvch uhlov zovrenych priamkami p, q. Je teda MAP = pq.

Priamkami p, r możno polożif rovinu r; v polpriestore rP urcime podia axiómy VII na priamke s bod Q tak, aby bolo AP — BQ. Obdob-ne polożime priamkami q, s rovinu n a urcime na priamke r v polpriestore 7t M taky bod N, aby platilo AM = BN.

Obrazce APQB a AMNB su rovnobeżniky, a preto plati PQ \ | AB, AB || MN, t. j. podia vety 1 aj PQ | | MN. Rovina rovnobeżiek PQ, MN pretne rovnobeżnć roviny APM, BQN v dvoch rovnobeżnych priamkach PM, NQ (pozri vetu 3). Je teda aj obrazec PMNQ rovno-beżnik, t. j. PM = QN.

Pretoże pre trojuholniky APM, BQN plati:

AP = BQ, AM = BN, PM = QN, je

A APM A; A BQN (sss),

t. j.

<£ pq = MAP = NBQ = rs, a to sme mali dokazaf.

Ostava dokazaf vetu 12 v pripade, że q = cr. Tu si zYolime pomocnu rovinu r rovnobeżnu s ro\dnou a, ale róznu od roviny q. V rovine r zostrojime priamky u || p, v || q. Pre ostre alebo prave uhly priamok p, q;r,s a u,v platia podia predchadzajuceho vysvetlenia vztahy

•$. pq = •$. uv, rs = <£ uv; preto je pq = rs, a tym je veta 12 celkom dokazana.

Teraz vyslovime novu definiciu.

Definicia. Nech p a q su dve na seba kolme róznobeżky. Potom hovorime, że smer p je koimy na smer q.

Z vety 12 vyplyva, że kolmosf dvoch smerov nezavisi od toho, ako zvolime obidve róznobeżne kolmice v tychto smeroch.

I)alej budeme pisat a J_ b pre dva kolme smery a aj cjs ak je r IubovoInou priamkou smeru a a s IubovoInou priamkou smeru b. Każdu priamku smeru a budeme nazyvaf kolmicou na każdu priamku smeru b.

Tymto je zavedeny pojem kolmic (a ^naćka J_) aj pre priamky, które su mimobeżne. Nebezpecie zameny so starym nazvom tu ne-vznikne, pretoże v pripade róznobeżnych priamok splyva novy nazov a oznacenie so starym nazvom.

Teraz si budeme definovaf dalsi pojem, a to kolmosf priamky a ro-viny.

169