1954 Geometria 014

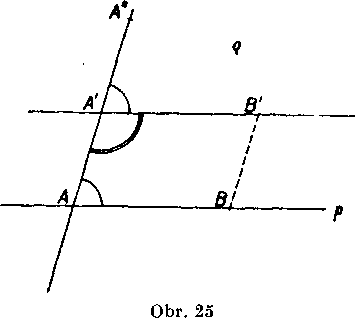
Nech su dane dva navzajom różne body A, A' (obr. 25). Na pre-dlżeni usecky AA' za bodom A' zostrojime bod A" tak, aby platilo A'A" = AA' a oznacime n jednu z polrovin s hranicou AA'. Podia

zakladnej vety o zhodnosti (poucka (5)) existuje jedine premiestenie. roviny, które prevadza bod A do bodu A', bod A' do bodu A" a pol-rovinu q do tej istej polro-viny o. Toto premiestenie volamo roYiiobeznym posu-nutina aiebo strucne posu-nutim.

Posunutie ma tieto dve hlavne vlastnosti:

(a)    preradza kaZdu priam-ku do priamky, która je s ftou rovnobeZna (odtial je-ho nazov);

(b)    yzdialenosf vzoru a obrazu je pri posunuti pre v§et-ky body roYiny ta ista.

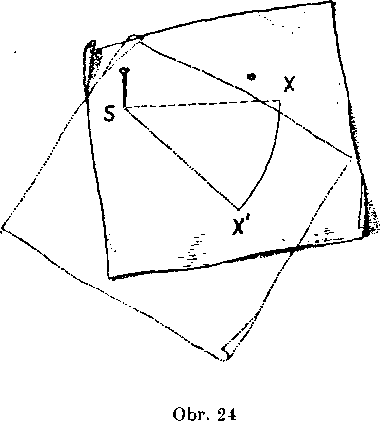
Obidve vlastnosti si overime, ak znazornime posunutie pohybom priesvitneho papiera po podloźke. Priesvitny papier premiestime tak, aby bod A presiel do bodu A' a bod A' do bodu A"; priesvitny papier

neobratime naruby, a tak pri tomto premiesteni prejde polrovina q do tej istej polroyiny c>. Z tohto znazornenia vyplyva, że posunutie je zhodnosf priama.

Ylastnosti (a), (b) vśe-obecne nebudeme doka-zovat; ich platnost si ukażeme iba na prikla-doch.

Je napr. zrejme, że priamka AA' prejde do priamky A'A" ćiże sama do seba; priamka AA' a jej obraz su teda rovnobeżne. Na obr. 25 je dalej priamka p, która pretina priamku AA' v bodę A. Vo vnutri pol-roviny g je na priamke p zvoleny bod B; jeho obraz, który tież leżi vo ynutri g, je oznaceny B’. Podia vlastnosti zhodnosti je

,    A'AB = <£ A"A'B’;

pretoże uhly <£ A"A'B' a <£ AA'B' su yedlajśie, je <£ A"A'B' -f-+ <£ AA 'B' = 2B; alebo

<£ A'AB + AA'B' = 2R.

Podia znamej vety (pozri str. 10) je AB\\A'B', eiże p\\p'\ to znamena, że priamka p ma vlastnost (a).

Stvoruholnik ABB'A' je rovnobeżnik, pretoże AB || A'B', AB = = A'B' a usecky AA', BB' sa nepretinaju (body B, B' leżia vo vnutri połroviny g). Preto je

AA' = BB',

ćo znamena, że bod B ma vlastnost (b). Roynaka uvaha plati pre ktorykolyek bod priamky p.

Cvicenie

1.    Dokażte, że priamky BE, FC v cvić. 10 clanku 1/2 su navzajom kolme.

2.    Zostrojte trojuholnik ABC, priesecik jeho yyśok a jemu opisanu krużnicu. K prieseciku yyśok zostrojte body sumerne zdrużene podia priamok AB, BC, GA. Ak rysujete presne, padnu tieto tri body na krużnicu opisanu.

3.    Narysujte IubovoIny śtyoruholnik P a dve priamky o_v o₂ nayzajom kolme. Zostrojte śtyoruholnik Pj sumerne zdrużeny s P podia priamky o_x a potom śtyoruholnik P₂ sumerne zdrużeny s P_x podia priamky o₂. Presvedcte sa, że śtvoruholniky P, P₂ su sumerne zdru-źene podia priesecika priamok o_v o₂.

4.    V sumernosti podia stredu każda priamka prejde do priamky rovno-beżnej. Dokażte to.

5.    Narysujte śestuholnik, który nie je pravidelny, ale je sumerny podia stredu.

6.    Narysujte śestuholnik, który nie je pravidelny, ale je sumerny podia osi.

15