1954 Geometria 192

Body, ktoró su svojimi ylastnymi obrazmi pri danom zobrazeni, yolame samodruźnymi bodmi v tomto zobrazeni. Z definicie ihned vyplyva:

Body royiny sumerncsti su jedine samodruźne body v sumerncsti podia roviny.

Nech je teraz X IubovoInym bodom a X' jeho obrazom v sumer -nosti podia roviny n. Povaźujme bod X' zayzor a hladajme jeho obraz v tej istej sumernosti podia royiny. Z konstrukcie uvedenej v de-finicii hned’ vidiet, że dostaneme znovu bod X.

VzhIadom na tuto ylastnost yystupuju ysetky body priestorn, które nie su samodrużne, vo dvojiciach, v których móżeme ktory-

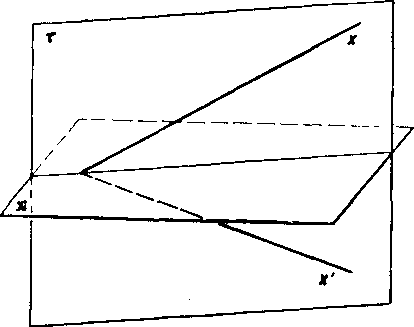
kol’vek z obidvoch bodov povażovat za vzor a dru-hy dostaneme ako obraz. Obidva body dvojice na-zyvame sumerne zdruże-nymi podia roviny 71.

Ak je dana nejaka mnożina bodoy, t. j. ne-jaky geometricky utvar U, tvoria obrazy bo-dov utvaru U v sumernosti podia roviny opat mnożinu, t. j. opat nejaky utvar U', ktOry nazyya-me obrazom utvaru U v danej sumernosti. Obi-dva utvary U a U' mó-żu byt totożne. V tomto pripade nazyyame utvar U utvarom samo-drużnym v danej sumernosti.

Ak je U = U', hovorime, że utvary U a U' su sumerne zdrużenó podia roviny n, lebo jeden je znovu obrazom druheho.

Napr. obidya polpriestory, oddelene rovinou n, su sumerne zdrużenó podia roviny 71, kdeżto rovina 71 je sama samodrużnym utyarom. Aj cely priestor (t. j. mnożina ysetkych bodov v priestore) je samodrużnym utyarom, a to v sumernosti podia której koIvek royiny.

Teraz budeme skumat najjednoduchsie geometricke utvary vo yzta-hu k rovinovej sumernosti, ćim ziskame najdóleżitejśie ylastnosti tohto zobrazenia.

Yeta 26. Obrazom priamky (ako mnożiny bodov) v sumernosti podia roviny je opat priamka.

Dokaż (obr. 46). Ak je priamka x kolma na rovinu sumernosti n, jej obrazom je zrejme ta ista priamka. Ak nie je x 71, potom podia vety 21existuje rovina t J_ n, która obsahuje priamku x. Obrazom priamky x v osovej sumernosti s osou p = co.t je urcita priamka x'\ ta ista priamka je obrazom priamky x v sumernosti podia royiny n.

O priamkach samodrużnych v rovinovej sumernosti plati tato veta.

Veta 27. Jedine samodrużne priamky v sumernosti podia royiny n su kolmice na rovinu n a priamky royiny n.

Dokaż. Nech je x = x' samodrużna priamka. Bud priamka x obsahuje aspon jeden bod A, który nie je samodrużny, potom obsahuje aj bod 4' i 4 a splyya podia axiómy I s priamkou AA', która je kolma na rovinu tz; bud’ priamka x obsahuje len samodrużne body a potom leżi v rovine n.

Uvedene priamky su skutocne samodrużne.

Obdobnym postupom ako vo vete 26 możno dokazat dalśie vlast-nosti sumernosti podia royiny: obrazom polpriamky je polpriamka, obrazom usećky AB je useeka A'B' s ńou zhodna.

Yeta 28. Obrazom royiny (ako mnożiny bodoy) v sumernosti podia royiny je zasa rovina.

Veta 29. Jedine samodrużne royiny v sumernosti podia royiny su sama rovina n a ysetky royiny na ńu kolme.

Vetu 28 a 29 nebudeme dokazovat, ale poużijeme ich v cviceniach.

Poznamka. Vśimnime si, że samodrużne utyary su dyojake. Priamka, leżiaca v n je samodrużna tak, że każdy jej bod je samodrużny; priamka kolma na n ma jedińy samodrużny bod, ostatne body tvoria dyojice bodov sumerne zdrużenych podia roviny 71 a priamka je samodrużna len ako celok (ako mnożina bodov). Obdobne smer koimy na 71 je samodrużny tak, że każda jeho priamka je samodrużna, kdeżto smer rovnobeżny s 71 je samodrużny len ako celok (mnożina priamok) a jeho jednotliye priamky — pokial neleżia v n — nie su samodrużne, leż tvoria dyojice sumerne zdrużenych priamok..

Całej si zavedieme nazov, który ste v obdobnom yyzname poznali uż v rovinnej geometrii a który sa vśeobecne poużiva v praxi.

Definicia. Utyar je sumemy podia danej royiny, ak sumernostou yzhladom na tuto rovinu prechadza sam v seba (je samodrużny

193