1954 Geometria 210

su vśetky zhodne a rovnoramenne. Preto polpriamky A_x0, A₂0, .., A_n0 su osami ynutornych uhlov pravidelneho w-uholnika.

Stredom krużnice ypisanej prayidelnemu w-uholniku je bod 0. Preto krużnica ypisana je sustredna s krużnicou opisanou. Spolocny stred obidyoch krużnic yolame stredom pravidelneho w-uholnika (obr. 63). Pretoże vśetky trojuholniky, z których sa składa pravidelny n-uholnik, su rovnoramenne, leźi bod O na osiach stran w-uholnika. Preto kruż-nica ypisana dotyka sa stran w-uholnika v stredoch 8_±, S₂,, S_n tychto stran.

Poznamka. Ak je prayidelnemu n-uholniku M opisana krużnica k, obratene poyieme, że w-uholnik M je ypisany do krużnice k. Podobne, ak je n-uholniku M ypisana krużnica k, hoyorime, że n-uholnik M je

><4

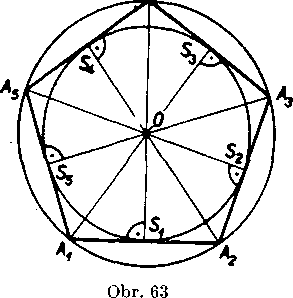
opisany krużnici k. Polomer krużnice w-uholniku opisanej budeme dósledne oznacoyat pismenom r, polomer krużnice ypisanej budeme oznacovat pismenom o.

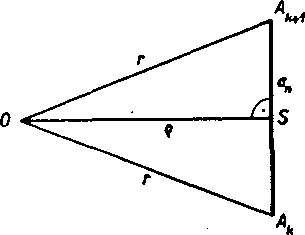
Yśimneme si jeden z rovnoramennych trojuholnikov, z których sa składa pravidelny Ji-uholnik. Oznaćme tento trojuholnik A OA_kA_k+1 (obr. 64; k je niektóre z cisel 1,2,    A_n+1 = A_x). Vrchol O je spo-

locnym stredom krużnice opisanej a ypisanej n-uholniku. Zakladnou A_kA_kĄ.₁ tohto trojuholnika je strana w-uholnika. Rameno OA_k — = OA_k+1 = r je polomerom krużnice opisanej, vyska 08 = £> je po-lomerom krużnice ypisanej.

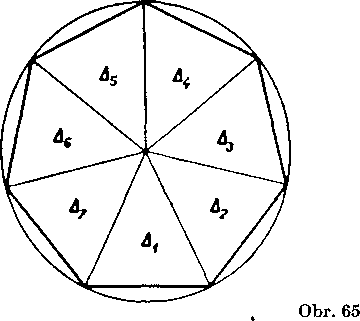
Ak zostrojime k prayidelnemu w-uholniku podobny iitvar, je aj tento utvar prayidelnym w-uholnikom (obr. 65).

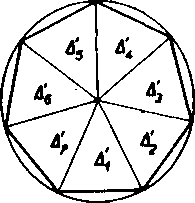
Dany w-uholnik móżeme totiż rozlożit na n zhodnych roynoramen-

nych trojuholnikoy Ai> A2> ____> A»- Ak ku każdemu z tychto troj-

uholnikoy zostrojime trojuholnik podobny, t. j.

Al ~ Ai,

A2 ~ A₂>

Aś ~ A3,

su aj trojuholniky A^, A^, Ań zhodne a roynoramenne, także utvar z nich zlożeny je pravidelny n-uholnik podobny danemu prayidelnemu w-uholniku. Dokazane tvrdenie możno vśak obratif, t. j.plati:

Veta 33. Każde dva prayidelne w-uholniky su podobne. Inak pove-dane:

Ak su dane dva prayidelne w-uholnlky, możno jeden z nich premiestif tak, aby existovala roynolahlost, która ho preyadza do druheho n-uhol-nika.

Dókaz. Nech su M, M' dva prayidelne ra-uholniky (obr. 66). Pre-miestime w-uholnik M' tak, aby jeho stred O' splynul so stredom O n-uholnika M a aby polpriamka 0'A{ splynula s polpriamkou OA₁ a bod A₂ padol do polroviny OA₁A₂. Potom ostatne polpriamky 0'Aź> 0’A₃,0'A_n splynu s polpriamkami OA₂, OA₃, ..., OA_n (każdy z uhlov A/JA₂, <£ A₂OA₃,A_nOA₁ aj z uhlov A{0’A₂,

47?

AA₂0’A₃,Alfi'A'_xma yelkosf —).

Th

211