1954 Geometria 158

Priklad 6. Je dany smer a a priamka b, która do neho neprislucha, Mamę dokazat, źe vśetky priamky smeru a, które su róznobeżne s priamkou b, vyplnia rovinu.

Vyrok „mnożina priamok yyplni rovinu“ chapeme takto: każda priamka mnożiny leźi v tej to rovine, a obratene: każdy bod tej to roviny leżi na niektórej priamke mnożiny,

Riesenie. Zvolime urcitu priamku a₀ smeru a rovnobeżnu s priamkou b. Priamky a₀, b inciduju podia vety 2 s jedinou royinou, ktoru oznaćime q. Każdym bodom roviny o prechadza jedna priamka smeru a; tu su vsetky priamky smeru a roynobeżne s priamkou b, lebo każdym bodom priamky b prechadza podia vety 4 jedina priamka smeru a.

Priklad 7 (obr. 19). Je dana kocka ABCDA'B'0'D' v zakladnej polohe. Yo vol'nej projekcii zostrojte priecku mimobeżiek AB, CB_/

smeru a) AG', b) DB'.

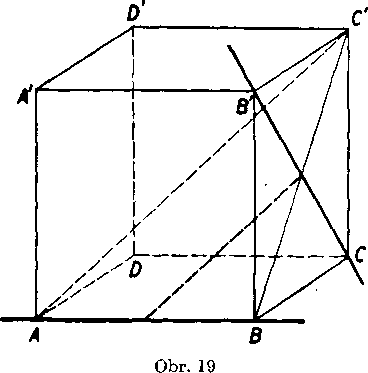
Rieśenie. a) Ak exis-tuje hladana priecka, leżi podia vysledku prikladu 6 v rovine urcenej priam-kami AB, AG’. Tato ro-vina ABC pretne rovi-nu rovnobeżnika BCCB' v priamke BG'. Hladana priecka prechadza teda priesecikom priamok B'G, BC, t. j. stredom rovno-beżnika BCCB' a je rov-nobeżna s priamkou AC".

b) Obdobnou uvahou ako v ulohe a) dójdeme k zaveru, że hladana priecka leżi v rovine B'CD. Pretoże tato rovina nema s priamkou AB spoloćny bod, je uloha neriesitelna.

Teraz prejdeme k rovnobeżnosti rovin. Odvodime najprv kriterium rovnobeżnosti rovin, które sa casto poużiva.

Veta0 Ak obsahuje rovina a dve priamky p, q nayzajom roznobezne, z których każda je rovnobeżna s rovinou q, potom je rovina a rovno-beźna s rovinou q.

Dokaż. E.oviny q, a bud’ nemaju spolocne body, a potom je poućka spravna. Bud’ maju spoloćny bod, potom musime dokazat, że splynu.

Ak maju roviny g, a spoloćny bod, maju spoloćnu priamku a. Priamka a je róznobeżna aspoń s jednou z priamok p, q, napr. s priamkou p. Kedze je p ]] g a okrem toho ma priamka p s rovinou o spoloćny bod a.p, leżi p v rovine g. No dvoma róznobeżkami a, p je urćena podia vety 2 jedina royina. Preto roviny o. a splynu, ćiźe su tież roynobeżne.

Rovnobeżnost rovin je vztah rovnako tranzitirny ako roynobeż-nost priamok. To vyjadruje nasledujuca yeta:

veta<^Ak je royina o roynobeżna s royinou a a rovina a roynobeżna s royinou r, je royina o roynobeżna s royinou t. Strucne: ak je g ]| a,

a||r, jep||r.

Dókaz. Ak splynu niektóre dve z rovin o, a, r, je yeta 9 zrejma. Ak su roviny g, a, x navzajom różne, musia mat podia vety 3 vzajom-nu polohu 1, lebo v nijakom inom z piatich uvedenych pripadov nie su dve dvojice rovnobeżnyeh rovin.

Veta Ysetky priamky, które prechadzaju danym bodom 4 a su roynobeżne s danou royinou g, yyplńaju royinu a || g.

Dókaz. Ak leżi bod A v rovine o, je yeta zrejma. Ak leżi bod A mimo roviny o, vedieme nim dve urćite różne priamky p || g, q ]| g a l’ubovoInu dalsiu priamku x || g. Roviny pq, px su obidve podia vety 8 roynobeżne s rovinou g, a preto su podia vety 9 roynobeżne nayza-jom. Kedze vśak maju spoloćny bod A, splynu, t. j. priamka x leżi v royine a = pq.

Dóleźity dósledok poućky vety 10 je tato poućka:

Yeta (Q). Danym bodom A v priestore możno k danej royine viesf jedinu roynobeżnu rovinu.

Dókaz. Źe taka rovina a existuje, dokazuje nam veta 10. Ostava dokazat, że je jedina. Oznaćme si r Iubovol’nu rovinu, która prechadza bodom A a je roynobeżna s royinou g. Każda priamka roviny r, która ide bodom A, je roynobeżna s royinou g \ preto roviny t, a splynu. Veta yyjadruje, że roynobeżne roviny maju obdobnu zakladnu ylastnosf ako roynobeżne priamky (pozri vetu 4).

Priklad 8. Dokażte poućku: Ak je priamka p roynobeżna s dvoma róznobeżnymi rovinami g, a, je roynobeżna s ich priesećnieou g.a.

Riesenie. Priamkou p ved’me rovinu t tak, aby bola róznobeżna s royinou pis royinou a. Oznaćme priesećnice r = g.r, s s a. r. Podia vety 5 je p\\r, p H •?, podia vety o tranzitivnosti rovnobeż-nosti priamok je r || s. Z yety 3 yyplyya, że royiny g, a, x maju bud

159