1954 Geometria 080

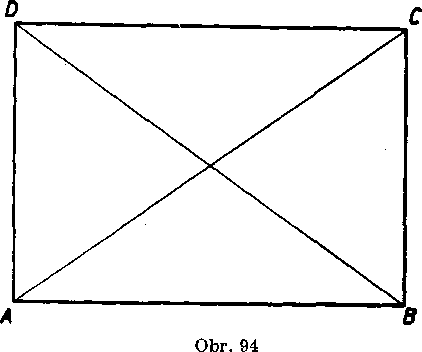
Priklad 11. Obdlżnik ma rozmery 12,3 cm, 8,7 cm. Mamę vypo-citat yelkost (ostreho) uhla, który zviera uhlopriecka a dlhsia strana.

Rieśenie (obr. 94). V obdlżniku ABCD je AB — 12,3 cm, BC = — 8,7 cm. Uhly, których yelkost hladame, su CAB, DBA, <£ ACD, BDC; vsetky tieto uhly su navzajom zhodne. Z pravo-uhleho trojuholnika ABC vyplyva

RG

* * °AB = -25'

ćiże

tg <£ CAB = ^ .= 87 : 123.

Pomocou tabulky obratenych cisel zistime, że

tg^CAB z= 0,7073

a z tabulky hodnót tangens dostaneme

<£ CAB = 35°16'.

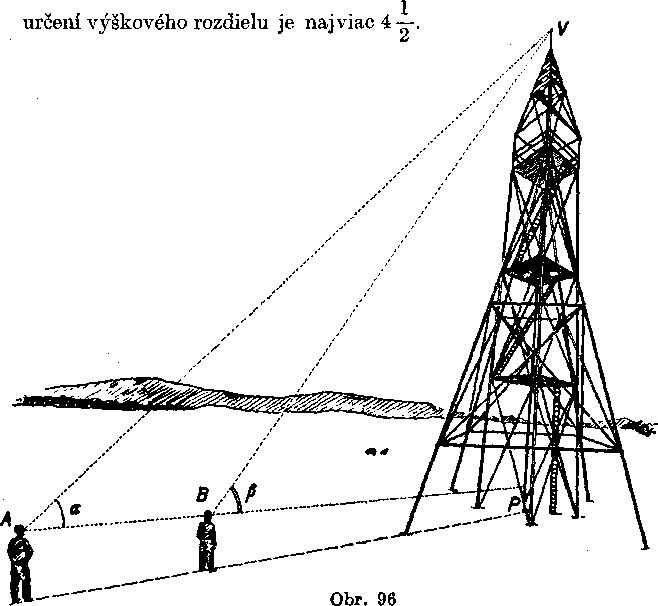
Priklad 12.Priama cesta z miesta A do miesta B stupa pod. uhlom 2°30' (obr. 95). Vodorovna (y praxisa hovori horizontalna), z mapy urcena vzdia-lenost miest A, B je 3,8 km. a) 0 kolko m je miesto B yyśśie neż miesto A\ b) S akou chybou urcime yyśko-vy rozdiel obidyoch miest, ak z mapy vy-ćitame vzdialenost AB s chybou 100 ml

Rieśenie. a) V prayouhlom trojuholniku ABC je znama yelkost uhla <£ BAG = 2°30' a yelkost odvesny AG = 3,8 km = 3 800 m. Mamę yypocitaf yelkost druhej odvesny BC.

Plati

tg<ZBAC = ^j-;

BC = AG.tg^BAG.

z tołio Ćiselne

. BCd=Z 800.0,0437 = 166, vyskovy rozdiel je teda asi 166 m.

Obr. 95

b) Ak pri uróeruvzdialenosti z mapy pripustime chybu 100 m, je sku-toćna yzdialenosf v medziach 3,7 aż 3,9 km. Prislusne vyśkove rozdie-

ly vypocitame ako v ods. a); su pribliżne 16I-i m, 170 — m. Chyba pri

Li    Li

81