1954 Geometria 116

Priklad 6. Na priamke AB mamę zostrojit vsetky body X, które spinaj u vzfah

= p.

AX

BX

Rieśenie. V oddiele II. riesili sme podobnu ulohu vypocitanim dlżok AX a BX; teraz ju vyriesime na zaklade rovno!ahlosti. Je zrej-me, że hladane body X móżu leżaf iba vo vnńtri usecky AB a na jej predlżeni za bod B. Pretoże pre każdy bod Y, który leżi na jej predl-

AY

żeni za bod A, plati AY < BY, ciże < 1, nemóże teda byt

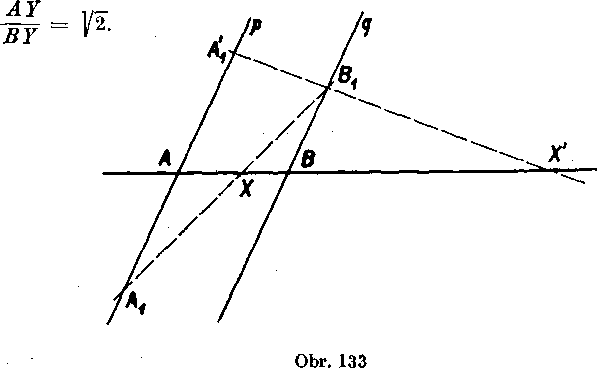
Obr. 133. Yedme bodmi A, B dve różne rovnobeżky p, q\ na priamke q zvo!me bod B_x ^ B a usecku BB_X povażujeme za jednotkovu. Ak je X hladany bod, który leżi vo ynutri usecky AB, potom roynolahlost so stredom X a s koeficientom — ]/¥ prevadża bod B do bodu A, sueasne prevadza bod B_x do urciteho bodu A_x a ma tieto vlastnosti:

(1)    bod A_x leżi na priamke p, pretoże p je obrazom priamky q;

(2)    body B_v X, A_x leżia na priamke; a to bod X leżi medzi bodmi A_v B_v preto priamka AB oddeluje body A_v Bp,

(3)    plati AA_X = ) — ]/2 ] . BB_X = ]/2.

Z toho vyplyva konstrukcia bodu X: na priamke p zostrojime bod Ap, prieseóik priamok AB, A_XB_X je bod X.

Podobne zostrojime hTadany bod X' na predlżeni usecky AB za bod B. Na priamke p zostrojime bod A{ tak, aby bolo AA{ = = ]/2 a aby bod A[ leżał v polrovine ABB₁ (obr. 133). Priamky AB, A_XB_X sa pretnu v bodę X'.Potrebne je pozń&menat, żeniejeAB \\A[B_X; keby tomu bolo tak, boi by utvar ABB_XA[ rovnobeżnikom a platilo by A Al = BB_X = 1, co je v rozporę s rovnosfou AA[ = ^2-Dana tiloha ma teda dve rieśenia.

U

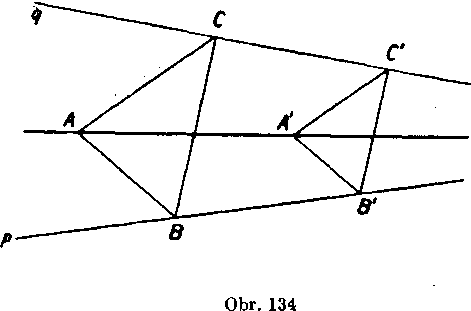
Priklad 7. Na obr. 134 su dve róznobeżky p, q, które sa pretnu mimo nakresne. Bod A marne spojit priamkou s ich nedostupnym priesecikom.

Rieśenie. Na priamkach p, q zvo!me body B, C tak, aby vznikol trojuholnik ABC; okrem toho zvoIme na priamke p eśte bod B'. Po-vażujme nedostupny priesecik M priamok p, q za stred rovnol’ahlosti, która prevadza bod B do bodu B'. Tato rovnoIahlosf prevedie trojuholnik ABC v urcity trojuholnik A'B'C' a ten vieme zostrojit. Bod C' leżi totiż na priamke q a je B'C || BC. Bod A' dostaneme tak, że bodmi B', C vedieme po poriadku rovnobeżky s priamkami BA, CA; obe tieto rovnobeżky sa pretnu v bodę A'.

Podia definicie rovnoIahlosti prechadza priamka AA' bodom M; priamka AM je teda zostrojena.

O rovnoIahlosf sa opiera pristroj, którym zvacśujeme alebo zmen-Sujeme rovinne utvary. Nazyvame ho pantograf.

Nech je dana rovnoIahlost so stredom S as koeficientom X, pre który plati 0 < X < 1. ZvoIme bod X $ S a zostrojme trojuholnik /SL4X

117