1954 Geometria 156

Tato poucka plati aj v stereometrii. Oznacme p danu priamku a A dany bod. Bod A leżi bud' na priamke p, a potom jedina rovnobeżka s priamkou p, która prechadza bodom A, je priamka p sama.

Bud’ bod A leżi mimo priamky p. Potom rovnobeżka s priamkou p a prechadzajuca bodom A musi leżat s priamkou p v tej istej rovine; tato rovina je zrejme rovina Ap, która je podia axiómy III jedina. V rovine Ap możno vśak viest bodom A podia znamej vety z planimetrie iba jedinu rovnobeżku s priamkou p.

Veta 5. Ak je priamka p rovnobeżna s rovinou g, potom każda rovi-na a, obsahujuca priamku p a róznobeżna s roYinou g, pretne rovinu g v priesecnici q . a rovnobeżnej s priamkou p. Każde dve z priesecnic g. a su navzajom roynobeżne.

Veta 5 je zrejma, ak leżi priamka p v rovine g. Ak neleżi priamka p v rovine o, zvolime dve różne roviny a_lt a₂ obsahujuce priamku p a róznobeżne s rovinou o. Roviny g, a_v a₂ ^{811 v0} vzajomnej polohe 3 z vety 3; vzajomna poloha 5 je vylućena, lebo priamka p = a₁.a₂ nema s rovinou g spoloćny bod. Z toho vyplyva, że każde dve z prie-secnic o₁.a₂, g.a_v g.a₂ su navzajom rovnobeżne, a to sme chceli do-kiizat.

Z vety 5 1’ahko odvodime dalśiu vetu, ktoru spravidla poużiyame, ak cbceme zistif, ci dana priamka je rovnobeżna s rovinou. Tato veta ea preto nazyva kriterium rovnobeżnosti priamky a roviny.

Yeta 6. Ak je priamka p rovuobeżna s niektorou priamkou q roYiny g, je roYnobeżna s royinou g.

Dókaz. Ak je p :| q, potom bud’ priamka p spłynie s priamkou q a veta je dokazana, bud’ p, q nemaju spoloćny bod, a preto aj p, g nemaju spoloćny bod. Tym je veta dokazana.

f)alej dokażeme vetu, która vyjadruje tzv. tranzitivnost rovno-beżnosti priamok v priestore (lat. trans —cez, eo —idem, teda tranzi-tiYnost ■— możnost prechodu).

Yeta 7. Ak je priamka a rovnobeżna s priamkou b a ak je priamka b rovnobeżna s priamkou c, je priamka a rovnobeżna s priamkou c. Strucne: ak je a \ \ b a 6 | [ c, je a, \ \ c.

Dokaż. Ak leżia vśetky tri priamky v tejże rovine (a to nastanę aj v pripade, ked' niektóre dve z priamok splynu), je veta 7 znama poucka z planimetrie.

Móżeme sa teda pri dokaże obmedz.it na pripad, że priamka c leżi mimo FQviny g różnych rovnobeżiek a, b (obr. 17). Na priamke c

!zvofme bod M a oznacme a = aM, r = bM. Każde dve z rovln ó, a, t su na.vzajom róznobeżne, ale roviny q, a, r nemaju spoloćny bod, pretoże priamky a, b nemaju spoloćny bod. Preto su roviny o, a, x

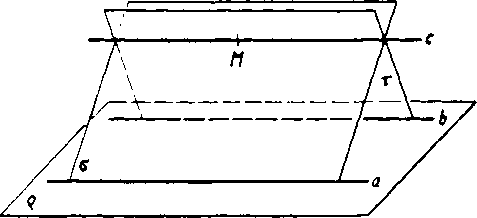
Obr. 17

vo yzajomnej polohe 3 z vety 3. Priesećnica a.r prechadza bodom M a je rovnobeżna s priamkou b\ taka priamka je vśak podia vety 4 jedina, a tou je priamka c. Podia vety 3 teda je a ]] r.

Napr. pri kvadri ABCDA'B'C'D' (obr. 18) vieme, że plati AB || CD, lebo ABCD je obdlżnik. Tak isto CD || C’D'. Podia vety 7 z toho vyplyva, że AB || C'D'. To    .    ,

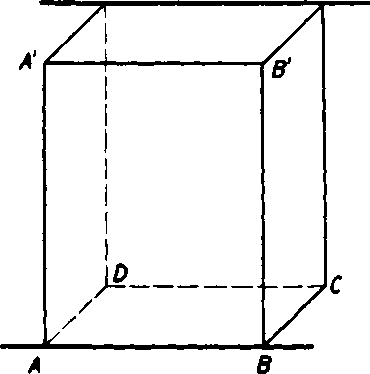
vśak je vlastnost, ktoru sme    “    C

pri kvadri poznali uż skór (rovnobeżnost protilahlych stran).

Tranzitivnost rovnobeż-nosti nam dovol’uje zaviest novy pojem. Mnożinu vset-kych priamok roynobeżnych s touże priamkou (a teda narzajom rovnobeżnych) na-zyvame smer. Każda priamka priestoru patri do jedi-neho smeru a każdy smer je urceny ktoroukol’vek svojou priamkou. Ak budeme ho-vori< o smere a, znamena to smer, do ktoreho patri priamka a.    Obr. 18

157