1954 Geometria 172

Predpokladajme, że existuje rovina q kolma na priamku p a pre-chadzajuca bodom A. Tato rovina q pretne roviny a, (i v dvoch priamkach a, b. Zrejme je a _[_ p, b J_ p a priamka a prechadza bodom A. Róznobeżkami a, b je vśak podia yety 2 urcena rovina jednoznacne. Rovina ab je podia yety 13 skutocne kolma na priamku p; tym je veta 14 dokazana.

Priamky a, b zostrojime takto: bodom A vedieme v royine a kol-micu a na priamku p; jej patou U yedieme v rovine /? kolmicu b na priamku p.

Predosla poucka sa tykała roviny kolmej na danu priamku. Je otazka, ci obratene na danu rovinu q możno danym bodom B viesf kolmicu, t. j. priamku kolmu na vśetky priamky roviny q a kolko je takych kolmic. Dokażeme najskór, że taka kolmica może byt najviac

jedna.

Dokaż urobime ne-priamo. Ak prechadza-ju bodom A dve różne kolmice k rovine q, potom ich rovina r je róznobeżna s rovinou q a pretina. ju v priam-ke s = q. r.

No potom v rovine r prechadzaju bodom B dve różne priamky kolme na priamku s, co nie je możne. Ostava teda dokazat iba exis-tenciu kolmic.

[VetaJ^ Danym bodom możno viest na danu rovinu jedinu kolmicu.

Dókaz. Podia toho, co sme vyśśie uviedli, staci kolmicu zostrojit. Pritom rozliśime dva pripady:

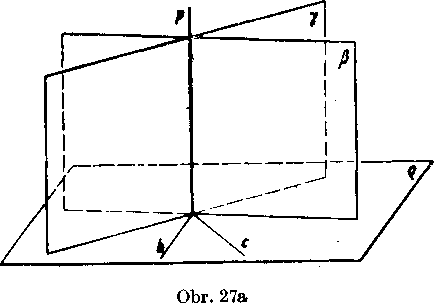
a)    Ak leżi dany bod A v danej rovine q (obr. 27a), yedieme bodom A v rovine q dve róznobeżky b, c. Podia vety 14 existuju roviny fi _L b, y J_ c, które obe prechadzaju bodom A. Roviny fi, y su róznobeżne, lebo maju spolocny bod A a nesplynu. Ich priesecnica p je kolma na priamku b aj na priamku c, a teda podia vety 13 je kolma aj na ro-vinu g.

b)    Ak neleżi dany bod A v danej rovine q (obr. 27b), zvolime v royine q priamku m a v royine Am yedieme bodom A kolmicu k priamke to; jej patu oznacime U. Bodom U yedieme v rovine o priamku k _L to a dalej v royine Ak yedieme bodom.A priamku p J_ fc.

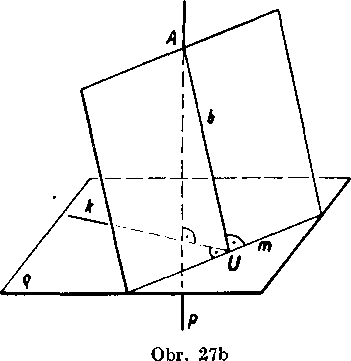
Royina Ak je podia vety 13 kolma na priamku to, lebo je ifJ Ito, k J_ to. Preto je aj p J_ to. Ale zo yztahu p J_ k, yi«i vyplyva podia vety 13 vztah p J_ q, który sme mali dokazat.

Postup v ods. b) predosleho dókazu udava zaroveń cestu, ako zostrojime kolmicu z bodu na rovinu: miesto jednej priamky to v rovine q poużijeme dve róznobeżne priamky m_v to₂; prisluśne kolmice k_v k₂ sa potom pretnu v bodę M hladanej kolmice (obr. 28).

. A

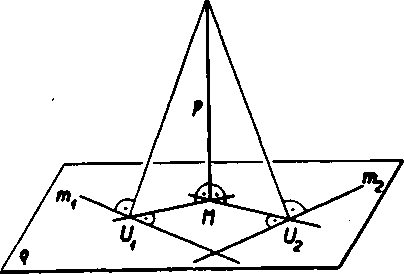
Obr. 28

Bod M nazyvame zyycajne patou kolmice.

Priklad 1. Je dana kocka ABCDA'B'CD' v za-kladnej polohe.

a)    Yo yolnej projekcii marne zobrazit patu P kolmice, yedenej bodom B' na rovinu A’C'B.

b)    Marne urcit skutoenu vel’kost usecky PB'.

Riesenie (obr. 29).

V royine A'C'B zyolime dve róznobeżky A 'B, A 'C' a bodom B' yedieme na ne kolmice v rovinach A'BB',

A'C'B'. Pretoźe obidva trojuholniky A'BB', A'C'B' su rovnoramenne s hlaynym yrcholom B', su paty U, V tycbto kolmic stredmi useciek

A'B, A'C'.

V rovine A'C'B yedieme body U, V kolmice po poriadku na priamky A’B. A'C’. Pretoźe trojuholnik A'BC' je rovnostranny, su tieto kolmice priamky VC', VB. Ich priesecik je hladana pata p.

173