1954 Geometria 178

kolma na prvu rovinu, t. j. że vztah kolmosti dvoch rovln je yzajomny. To vyslovimo presne vetou.

Veta 18. Ak je rovina a kolma na rovinu g. je rovina g kolma na ro-yinu-ff.

Dokaż (obr. 33). Mamę zrejme dokazat toto: Ak obsahuje rovina

a priamku p _[_ g, obsahuje rovina o

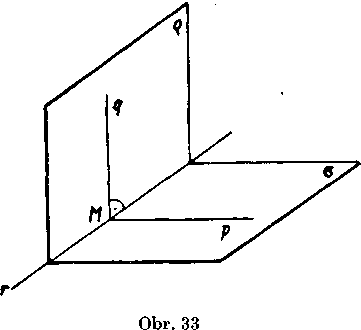
priamku q A Nech teda pre priamku p leżiacu v rovine a plati p J_ g. Oznaeme M prie-secik p q a r priesecnicu g. a. Priesecnica r aj bod M urcite existuju, pretoże roviny g a a nemóżu byt rovnobeżne. Priam-ka r prechadza bodom M. Bodom M v rovine g ved'me kolmicu q na priamku r. Pre priamku q plati nielen q J_ t, ale aj q J_ p, pretoże p _|_ g. Pretoże p a r su dve roznobeż-ky leżiace v rovine a, dalej plati, że q J_ o, co sme chceli dokazat. Preto zo vztahu o J_ g vyplyva vzfah g J_ a.

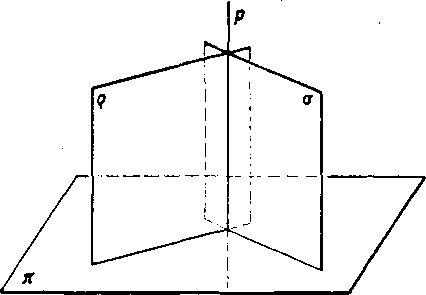
Z dókazu, który sme prave urobili, odvodime si este jeden dósledok. Poużijeme oznacenie tohto dokazu. Priamky p a q leżia v tejże rovine, pretoże obidve prechadzaju tym istym bodom M. Oznacime r rovinu priamok p, q. Pretoże je r j_ p & r _[_ q, je r t & z toho vyplyva g J_ r a aj er t. Tymto sme sa presvedcili o existencii troch rovin, z których każde dve su na seba kolme. Tieto roviny sa pretinaju v troch priesecniciach, które prechadzaju jednym bodom a każde dve z nich su na seba kolme. Takato poloha troch rovin v priestore je velmi dóleżita ako v teorii (stretnete sa s ńou napr. v rysovani), tak aj v praxi. Yyrobky różnych odvetvi priemyslu, na których su casti troch rovin v tej to polohe, najdete na każdom kroku. Uved’te sami niektóre priklady.

Z mnohych viet, które platia o rovinach navzajom kolmych, doka-żeme si len niektóre. Prvu z nich uvedieme bez dókazu.

Yeta 19. Ak su dve roviny navzajom kolme, prechadza każdym bodom jednej z nich jedina priamka kolma na druhu. Tato priamka je incidentna s prvou rovinou.

Veta 20. Ak su roviny g a a dve róznobeżne royiny a ak je każda z nich kolma na tu istó rovinu n, je ich priesegnica p = g.a kolmk na n.

Dókaz (obr. 34). Naprieseónici p = q.a zvolime bod Ma vedieme nim kolmicu na n. Podia vety 19 musi tato kolmica leżaf v q aj v a, t. j. musi splynut s priamkou p, cim je veta 20 dokazana.

Ak je priamka p kolma na rovinu n, vieme uź, że ńou możno yiest nekonecne mnoho rovin kolmych na n. Ked’ vsak priamka p nie je kolma na rovinu n, plati veta:

Veta 21. Ak priamka p nie je kolma na rovinu n, możno nou yiesf jedinu royinu a kolmu na royinu n.

#1h. 14

Dókaz. Na priamke p (obr. 35) zvolime bod M a yedieme nim kolmi-eu q na jt. Priamky pa,q su rózńe, pretoże p nie je kolmicou na rovinu n, a preto ureuju priamky p, q jedinu royinu a. Rovina a obsahuje priamku q _L n, a preto je a J_ n. Rovina a je jedina rovina kolma na n a obsahujuca priamku p: pretoże keby bola este ina rovina a', obsahu-juca priamku p, pre ktoru by platilo a' J_ musela by byt podia vety 20 priesecnica p = a.a' kolma na royinu n. To je vśak v rozporę s predpokladom.

Dosial sme zobrazovali priestorove utvary (napr. telesa) do roviny vo voInom rovnobeżnom premietąni. V rysovani sa oboznamite s inym sposobom. Nazyyame ho pravouhle premietanie a zhruba sme ho pre-berali uż v 8. rocniku.

V stereometrii vyslovime iba zakladnu definiciu a uyedieme dve yety.

179