1954 Geometria 254

Z podmienky [3] definicie obsahu vyplyva, ze obsah lichobeżnika ABCD je

1    ,1    Z, + 2_S

2^ + 7 ^z*^v = u-

Pretoże

je vel’kost strednej priecky lichobeżnika o zaklad-

niach z_v z,, możeme vetu 3 vyslovi£ aj takto:

Obsah lichobeżnika sa rovna sucinu veI’kosti strednej priecky a vyśky.

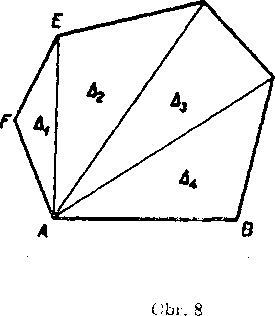
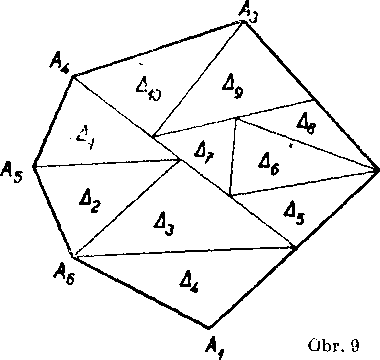
Poznamka. Ak chceme urcit obsah ]'ubovoineho w-nholnika, staci ho rozdelii nejakym sposobom na neprekryvajuce sa trojnholniky a urcit ich obsahy. Obsah daneho n-uhołnika rovna sa potom podia

Obr. 10

podmienky [3] (resp. podia poznamky 2) suctu obsahov tychto troj-uholnikov.

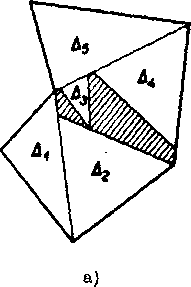
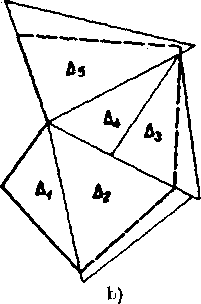
Rozlożifi n-uholnik na neprekryvajuce sa trojuholniky znamena zo-strojit konecny pocet trojuholnikov, których vśetky body vyplnaju dany n-uholnik. Take rozkłady su na obrazkoch 8 a 9. Naproti tomu trojuholniky Ai> • • •, As ^na obr. 1 Oa. b, netvoria rozkład mnohouhol-nika; odóvodńite prećo.

Nakoniec dokażeme stereometricku vetu, która vyjadruje vztah medzi obsahom mnohouholnika M leżiaceho v rovine q a obsahom jeho pravouhleho priemetu M' do roviny n róznobeżnej s q (obr. 11).

Veta 4. Nech ma mnohouholnik M, który Iezt v rovine o, obsah P. Ak tento mnohouholnik pravouhle premietneme do roviny n, która je rbznobeźnh, ale nie kolma na rovinu o- je obsah priemetu M'

P' = P.cosa,

kde a je odchyłka rovin n, n.

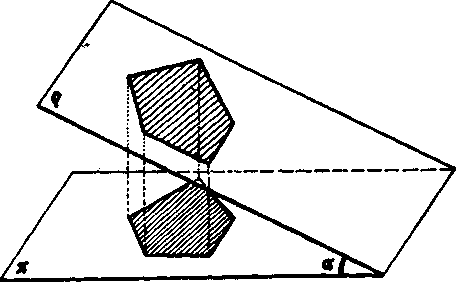
Obr. 11

Skór neż budeme dokazovat vetu, poznamenajme toto:

Ak su roviny n, v rovnobażne a ak premietneme trojuholnik A ABC leżiaci v rovine v pravouhle do roviny n, je priemetom trojuholnik l\A'B'C' zhodny s & ABC podia sss (obr. 12: A'B'BA, B'C'CB, CA'AC su totiż pravouhle śtyoruholniky, także A'B' — AB, B'C = = BC, CA' = CA). Trojuholniky A ABC, A A’B'C maju podia podmienky [2] rovnakv obsah.

Vetu 4 dokażeme v troch ćastiach. Najprv dokażeme, że veta plati, ak je mnohouholnikom M trojuholnik, ktoreho jedna strana je rovno-

255