1954 Geometria 064

Dókaz (obr. 77). Pravouhly trojuholnik ABC doplnime na rovno-ramenny trojuholnik ABD; urobńne to tak, że k trojuholniku BCA zostrojime trojuholnik BCD suniernc zdruźeny podia osi BC. Trojuholnik ABD je potom rovnoramenny, lebo AB = BD. Obdobne zostrojime rovnoramenny trojuholnik A'B'D'. Pre tieto rovnoramenne trojuholniky plati

A'B' B'D'

AB BD ~^k

a dalej

A'D'    2 A'C'    A'C' A'B'

AD ~ 2AC ~~ AC ~ AB ~

c'

c

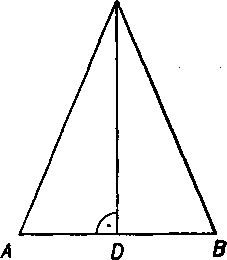
Je teda

A'B' = h. AB, B'D' = h.BD, A'D' = k.AD,

a preto A ABD ~ A A'B'D', Ai A ~ <f- A' a podia vety u u je A ABC ~ A A'B'C'.

Priklad 11. Dva rovnoramenne trojuholniky maju ramena s dlż-kami a, a' a vyśky na zakladne maju dlźky v, v'. Platia Yztahy

a. _ a' v v''

Mamę dokazat, źe obidva trojuholniky su podobne.

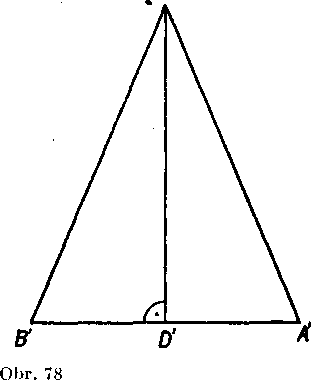
Riesenie (obr. 78). Ak oznaćime vrcholy obidvoch trojuholnikov A, B, C\ A', B', C' a stredy zakladni AB, A'B' pismenami D, D', je podia vety 5

	A ACD~	A A'C'D'.
Preto	A'B'	A'C
	AD	AC ’
ciże	2A'D'	A’C'
	2ad :	AC ’
ćiźe	c' __	a'
	c	a'

Tymto je podobnost obidvoch trojuholnikov dokazana.

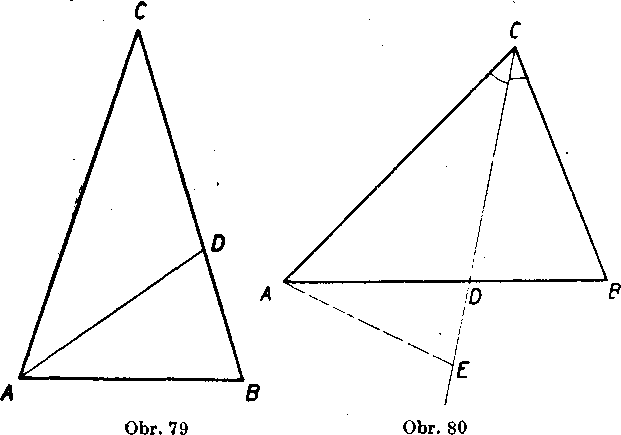
Cvicenie

1.    Ak je z dvoch podobnych trojuholnikov jeden pravouhly, je aj druhy pravouhly. Dokaźte to.

2.    VeIkosti stran trbjuholnika PQB su i-nasobky ve!kosti stran trojuholnika P'Q'R'. Y akom pomere su ich obsahy?

3.    Dane su trojuholniky ABC, A'B'C'\

65