1954 Geometria 306

ateda podia vety 4 (str. 255) je n = p cos*, kde p znamena obsah pod-stavy hranola. To znamena, że objem daneho hranola sa rovna nh = — ph cos*.

Najdeny yysledok dalej upravlme. Pretoże hrana hranola je kolma na rovinu kolmeho rezu a vyśka hranola je kolma na roviny podstay, odchyłka hrany a vyśky rovna sa oc. Ak je teda P pata vysky vedenej z vrcholu A' na rovinu podstavy ABGDE, uhol AA 'P v pravouhlom trojuholnlku APA' rovna sa *. Z toho vyplyva, ak oznacime veIkost yyśky hranola v, że v = h cos*. Teda objem daneho hranola sa rovna ph cos* = pv, ako sme mali dokazat.

Z postupu dókazu je zrejme, że veta piat! pre IubovoIny w-boky hranol.

Poznamka. Ak V znamena objem hranola, ktoreho podstava ma obsah p a vyśka ve!kosf v, potom tvrdenie vety 2 móżeme zapisat yzorcom

V = pv.

Cvićenie

V pravidelnom śtvorbokom hranole je znama jeho yyśka a odchyłka p telesovej uhlopriecky od podstavy; urcte objem telesa.

Ciselne:    v — 10 cm, cp = 60°,

i v = 25 cm, q> = 67J°.

2.    Z pravidelneho trojbokeho hranola s podstavnou hranou a sme dworni r J7n jbsżaymirezmi oirezali kosy trojboky hranol, ktoreho

bocne hrany maju veIkost 6. Urcte objem koseho hranola.

Rieśte aj pre

a)    pravidelny śtvorboky hranol,

b)    pravidelny śestboky hranol.

3.    Dokażte: Objem trojbokeho hranola rovna sa polovicnemu suSinu obsahu bocnej steny a jej vzdialenosti od protilahlej bocnej hrany.

4.    Kosy hranol ABCDA 'B'G'D' ma za podstayu śtvoruholnlk ABGD, ktoreho uhlopriecky su nayzajom kolme; rez AA'G'G je koimy na podstayu. Vyjadrite objem hranola poużitim uhlopriecky BI) a obsahu p rezu AA'C'G.

5.    Podstava śtvorbokeho hranola ABCDA'B'G'D' je kosośtvorec ABCD; BAD = 60°. Bocne hrany urcuju s podstavou uhol 60°, rovina AA'C'G je kolma na podstayu. Dokażte, że pomer obsahov osoyych rezov BB'D'D a AA'CG je 2 : 3.

6. Kosy trojboky hranol ABCA’B'C ma za podstayu roynoramenny trojuholnik ABC so zakladnou BG — a. Bocna hrana AA' yelkosti b je kolma na hranu BO. Uhol stien, które prechadzaju hranou AA' je «. Urcte objem hranola poużitlm hodnot a, b, <x. (Poużite koimy rez.)

7/Urćte objem trojbokeho hranola s podstavnymi hranami a, b, c a bocnou hranou h; uhol bocnej hrany s yyskou rovna sa x.

Olselne: h = 12, a = 13, b = 14, c = 15, « = 30°.

JŁ Kolko kg vażi 150 kusov mo-sadznych tyeiniektvarupravi-delneho sesfbokeho hranola s podstavnou hranou 6 mm a bocnou hranou 25 cm? Hu-stota mosadze je 8,1 gem^-3-

				$
	1	|ł
	120

Obr. 62

9. Kolko vaźi profilova ocel, 3,75 m*dlha, której priemer je dany (obr. 62, rozmery su v milimetroch; spec. vaha ocele je 7,8 gem^-3).

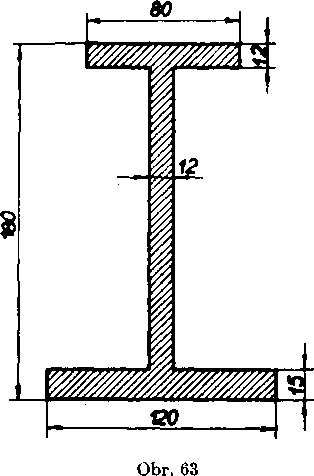
10> Urcte vahu valcovaneho nośnika, dlheho 4,22 m daneho priemeru (obr. 63, rozmery su v milimetroch; spec. vaha ocele je 7,8 gem"³).

Kolko m³ zeminy treba premiestif pri yykope priamej, 170 m dlhej \vodnej priekopy, której prierez ma tvar rovnoramenneho licho-beżnika o zakladniach 80 cm, 150 cm a vyśke 80 cm. S akou bez-pecnostou sa pocita pre mimoriadne stavy vody, ak je priemerna yyśka vody v priekope za normalneho stavu 25 cm ?

307