1954 Geometria 340

Ako dósledok tejto vety odvodime si dalśie vety, które nam umożnia rychlejśi yypoćet piasta hranola a prayidelnych ihlanoy.

Piast hranola rovna sa sucinu obvodu kolmeho rezu prisluśnej hra-nolovej płochy a dlżky boćnej hrany.

Dokaż (obr. 83) strany normalneho rezu A'B'C'D' hranolovej płochy prisluchajucej danemu hranolu. Obsah każdej z boćnych stien (z których każda je rovnobeżnikom) vyjadrime ako sućin zakladne a vyśky, prićom za zakladhu volime boćnu hranu hranola; yyśka sa rovna tej strane normalneho rezu, która leżi v rovine uyażovaneho rovnobeżnlka. Ak je dlżka boćnej hrany h, potom podia predoślej vety dostaneme pre piast

h.A'B' + h.B'C' + ... + h.E'A' = h{A’B' + B'C' -f ... + iTA'),

clm sme tvrdenie vety dokazali, pretoże vyraz v zatvorke rovna sa prave obvodu normalneho rezu (uvedeny je dókaz len pre patboky hranol; pre w-boky hranol je dókaz podobny).

Specialny pripad najdenej vety je veta:

Piast kolmeho hranola rovna sa sucinu obvodu jeho podstayy a vysky.

Dókaz vyplyva z toho, że podstava je normalnym rezom kolmeho hranola a vyska rovna sa dlżke bocnej hrany.

Bez dókazu uvedieme estc dalśie dvevety (ichplatnostdokażtesami).

Pląśt pravidelneho ihlana rovna sa polovicnemu sucinu obvodu jeho podstayy a boćnej vyśky.

Piast pravidelneho zrezaneho ihlana rovna sa polovićnemu sucinu zo sućtu obidvoch podstay a polovićnej vyśky.

Cvićenie

1.    Urcte povrch kocky metódou prikladu 1.

2.    Ako sa zmeni povrch kvadra, ak jeho rozmery postupne nasobime kladnymi ćislami h, Tc, U

3.    Meranim sa zistili rozmery a, b, c kvadra. Urcte medze pre hod-notu povrchu kvadra a) presne, b) pribliżne, ak pripustna merana chyba rovna sa e-nasobku meranych rozmeroy (e je dost małe yzhladom na rozmery kvadra).

4.    Ako sa zmeni povrch kvadra, ak vśetky jeho rozmery zvaćśime o hodnotu e (jej je mensia neź ktorykolyek z rozmeroy kvadra)? Urcte pribliżnu hodnotu prirastku (zmenśenie) tak, że yynechate yśetky cleny obsahujuce e vo yyśśej mocnine neż pryej.

5. Urcte povrch kvadra, ktoreho telesova uhlopriecka je u a ktoreho rozmery su v pomere p : q : r (p, q, r su kladne cisla).

,6_y Urcte povrch kvadra, ak poznate jeho objem F a ak su jeho rozmery v pomere h : k : l (h, k, l su kladne cisla).

Ćiselne: V = 1 dm³, h — 3, k = 5, l — 7.

7. Uhlopriecky stien kvadra prechadzajuce jednym jeho vrcholom su u_v u₂, u_z. Urcte povrch kvadra.

Ćiselne: % = 13, u₂ = 14, u₃ = 15.

87 Pravidelny ra-boky hranol ma podstavmi hranu a, vyśku v, povrch P a. objem F. Urcte zvysne prvky, ak je dane:

^ łl = 3, a = 10 cm, v = 15 cm;

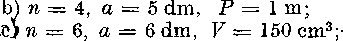
d)    n = 8, v — 0,5 m, V = 0,75 m³.

9. Objem koseho sesfbokeho hranola, ktoreho podstava je pravidelny sestuholnik o strane a, jeF. Bocne hrany maju odpodstavy odchylku a; koimy rez hranolovej płochy ma obvod o. Urcte povrch hranola.

Ćiselne: a = 2 dm, F = 60y3 dm³, x — 60° o = 10,5 dm.

10.    Dokażte, że povrchy podobnych ihlanov su v rovnakom pomere ako stvorce zodpovedajucich si hran.

11.    Urcte povrch śtvorstena, ktoreho dve steny su rovnostranne trojuholniky o strane a a śtvorsten leżi v ro\^rinach na sebakołmych.

12.    Pravidełny n-boky ihlan ma podstavnu hranu a, Pocnu hranu h, vysku v, povrch P a objem F. Urcte chybajuce prvky, ak poznate:

a)    n = 4, a = 5,7 cm, v — 13,2 cm,

b)    n = 3, a = 10 cm, h = 12 cm,

e) n = 6, a = 1,5 dm, F = 8 dm³, d) n = 4, v = 4,5 dm, P = 180 dmF

13.    Urcte piast ihlana, ktoreho podstava je rovnobeźnik-o stranach a, b a obsahu p. Pata kolmice vedenej vrcholom ihlana na podstavu prechadza jej stredom; vyska telesa je v.

Ćiselne: a = 20 cm, 6 = 36 cm, p = 36 cm², v = 12 cm.

14.    Urcte piast pravidelneho m-bokeho ihlana s bocnou hranou h, która ma od podstavy odchylku <x.

Ćiselne: n = 4, h = 8,5 cm, tx = 65°.

15.    Pravidelny zrezany w-boky ihlan ma podstavne hrany a₁, a₂ (a_x > a₂); bocna stena ma od podstavy odchylku«. Vypocitajte jeho povrch.

Ćiselne: n = 6, a,_x = 8,5 cm, a₂ = 6,5 cm, « = 60°.

341