1954 Geometria 102

AB dlżky d. Odsek vytina na osi usecky AB useóku GD vel'kosti v. Vyjadrite v ako funkciu r, d.

5.    Obdlżnik ma rozmery a, b, śtvorec —~ . Porovnajte dlżky ich uhlopriecok.

6.    Krużnica ma polomer r, jej tetiva dlżku d a vzdialenosf v od stredu krużnice.

a)    Yyjadrite yzdialenost v pomocou d, r\vypocitajte v pre d = 4,5 m, r = 6,7 m.

b)    Urćte tetivu, której dlźka sa rovna jej vzdialenosti od stredu. (VoIte r = 1).

7.    Rovnoramenny trojuholnik ma zakladhu dlżky a cm, rameno dlżky b cm.

^a)    Vyjadrite dlżku jeho vysky na zakladhu pomocou a, b.

b)    Vyjadrite jeho obsah pomocou dlżok a, b.

c)    Je dane a = 18 cm, b = 41 cm. Vypocitajte obsah trojuholnlka a dlżky YŚetkych jeho vyśok.

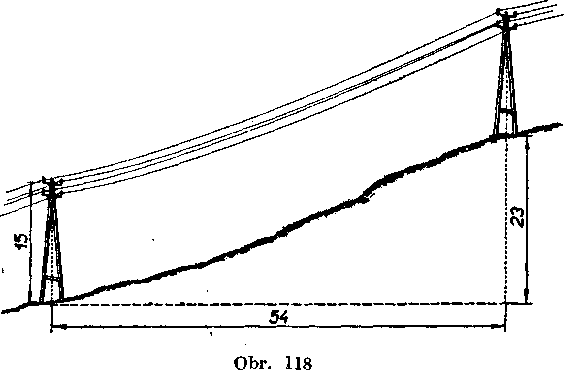
8.    Na obr. 118 su dva stożiare (nosice) diaIkoveho vedenia, 15 m vy-soke, vyśkovy rozdiel ich piat je 35 m, vodorovna vzdialenost je 134 m. Aka je dlżka vedenia medzi nimi, ak sa pocita na previsnu-tie 5 % drótu.

9.    Obr. 119. IJsecka AB = s predstavuje priamy usek trati, AC — h je vodorovna vzdialenost bodov A, B, BC = v je ich vyśkovy rozdiel.

Oznaćte p, q pomery ”,    —v percentach.

a)    Yyjadrite q pomocou p.

b)    Dokażte, ze q neprekroci 1%, kym p neprekroci 4%.

B

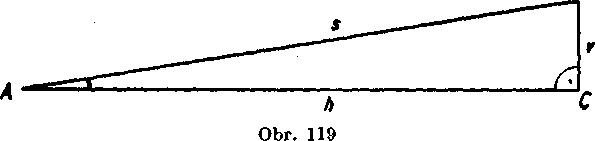
2. Konstrukcie algebr aicky cli vyrazov

Yztahy medzi stranami podobnych trojuholnlkov, najma veta Py-tagorova a vety Euklidove, nim umożnuju z os trój i t niektóre geomet-ricke utvary na zakłade predchadzajuceho vypoćtu. Celkom jedno-duchy pripad sme poznali v priklade, v ktorom sme zostrojili śtrorec toho isteho obsahu, aky mai dan<^r obdlżnik. Ukażeme si dva zloźitejsie

c

prlklady.

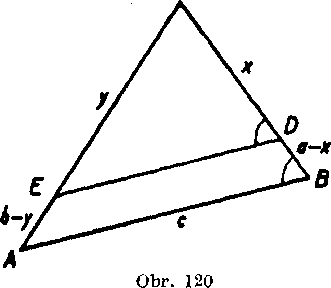
Prlklad 4 (obr. 120). V trojuholniku ABC marne viest priecku DE, rovnobeżnu so stranou AB tak, aby lichobeź-nlk ABDE a trojuholnik EDG mali rovnake obvody.

Rieśenie. VeIkost ńsećiek oznacme małymi plsmenami podia obr. 120. Dana podmien-ka o rovnakej dlżke obvodov potom znie:

(4) c Ą- a — x + b — y =

= x + y,

lebo strana DE je obidvom obrazeom spolocna. Zo vztahn (4) vyplyva

(5)

103