1954 Geometria 112

brat. Preberieme na ukażku iba pripad druhy a stvrty a pritom zvo-lime X = —

Vdruhompripade (obr. I28b)vidiefi, ie,A'B'\\ AB. Dalej je AB—SA —

—SB-,A'B'=SA' — SB' = ^r$A — ^rSB = \ (SA — 8B) = ^- AB.

£ £ £ £

V śtvrtom pripade (obr. 128d) je podlą vety su

A SAB ~ A SA’B',

ako v priklade 1. Z toho vyplyva, że A ’B' = — . A7i. Okrem toho je

A'B' || AB, lebo uhly BAS a <£ B’A’S su striedave, a teda zhodne.

Dókaz oboch pripadov nie je vśak este uplny. Mali by sme este do-kazafi, że obraz kaźdeho bodu usecky AB leżi na usecke A 'B' a obra-tene, że każdy bod usecky A'B' je obrazom niektoreho bodu usecky AB. Ide vlastne o to, że dve mnożiny bodov su totoźne: usecka A'B' a mnożina obrazov vśetkych bodov usecky AB. Toto tvrdenie nebu-deme dokazovat.

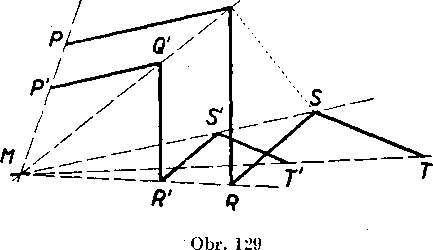
Priklad 2. K lomenej ciare z obr. 129 marne zostrojif rovno!ahly utvar podia stredu M, który nie je bodom tej t o eiary; koeficient rovno-2

1’ahlosti je X —

³ .

Rieśenie. Lomena ćiara sa składa zo styroch iiseciek PQ, QR, RS a ST. Podia vety 1 prevadza dana rovno!ahlosf tieto usecky po po-riadku v usecky P'Q', Q'R', R'S' a S'T'. Napr. najskór zostrojime obraz S’ bodu S; dalej zostrojime bod T' tak, aby body M, T', T leżali v priamke a aby bolo S'T’ || ST. Rovnako ako bod T' zostrojime aj bod i?'. Bod Q zostrojime na priamke MQ tak, aby bolo 8'Q' || SQ; pritom poużijeme na zaklade vety 1 pomocnu usecku SQ (na obr. 129 je óiarkovana). Rovnako ako bod Q' zostrojime aj bod P'.

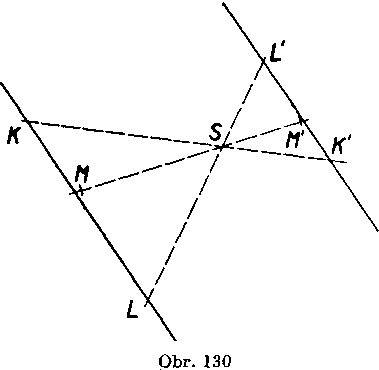
Priklad 3. (Obr. 130.)

Body K, L, M neleżia na priamke. Odóvodnime, że ani ich obrazy K', L', M' v rovno!ahlosti so stre-dom 8 neleżia na priamke.

(Overeniekonśtrukciou je • nespoIahlive.)

Riesenie. Nech md dana roynolahlosf koeiicient A. Body K, L, M móżeme povażovaf za obrazy bo-dov K', L’, M’ v rovno-lahlosti so stredom 8

a koeficientom — . Keby

body K', L', M’ leżali na

priamke, leżał by niektóry z nich medzi ostatnymi dvoma; napr. bod L’ leżał by medzi K', M'. Potom by podia vety 1 leżał aj bod L medzi bodmi K, L; body K, L, M by teda leżali na priamke, a to je v spore s predpokladom.

Priklad 4. Marne dokazaf, że rovnoIahlosf prevadza trojuholnik ABC v trojuholnik A'B'0', który je s danym podobny. .

Riesenie. Je to vlastne zovśeobecnenie yysledku prikladu 1; dókaz lahko urobime pomocou vety 1. Trojuholnik ABC sa składa zo vśet-kych bodov vsetkych useciek AX, kde bod X prebieha po usecke BC. Roynolahlost prevedie yrcholy A, B, C do bodov A', B', C', które neleżia na priamke (pozri pr. 3); usecku AX do usecky A'X'. Ak prebieha bod X po usecke BC, prebieha bod X' po usecke B'C'. Preto obrazy ysetkych bodov yśetkych usećiek AX yyplnia Ą A'B'C.

Dalej je podia yety 1: A'B[ = j X | AB, B'C = \X\BG, CA' =* = | A j CA, preto A A’B'C' ~ A ABC.

Możno dokazaf, że roynolahlosf prevadza priamku do priamky s ńou rovnobeżnej; dalej prevadza polpriamku do polpriamky, polrovinu do polroviny, uhol do uhla s nim zhodnóho. Tieto tvrdenia nebudeme dokazoyaf, ale budeme ich poużiyaf. Niektoró z nich si odóvodnite v cviceniach.

113