1954 Geometria 174

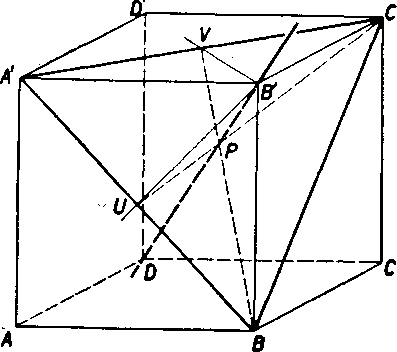
b) Bod P leżi na priamke BV, a teda i v royine BB'V. Priamka B'V prechadza bodom D', lebo V je stred §tvorca A'B'G'D'. Pretoźe priamky BB', DD’ su rovnobeżne, leżia body B, B', D, D', V, P v tejże

Obr. 29

rovine q = BB' V.

Rovina p pretne kocku v obdlżniku BB'D’D; je totiż BB' = DD', BD = = B’D', BB' Ą_BD, lebo priamka BB' je kolma na rovinu ABC.

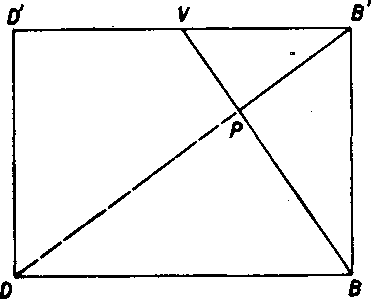
Na obr. 30 je zostro-jeny obdlżnik BB'D'D, stred V jeho strany B'D' a pata P kolmice vedenej bodom B' na priamku B V. Useeka B'P je tu v sku-toćnej vel’kosti.

Obr. 30

Poznamka. Ak sa spravne rysuje, leżi bod P na obr. 29 aj na obr. 30na priamke B'D. BodP je totiż zaroveńpatou kolmice yedenej z bodu D na rovi-nu A'C'B. Zistime obdobnu konśtrukciu ako v priklade la.

Ak si znova prezriete texty oboch predoślych viet 14, 15, iste vas uputa napadna zhoda medzi nimi. Staciy jednej zame-nit slovo ,,priamka“ slovom ,,rovina“ a naopak, aby sme dostali druhu. Uvedieme eśte jednu dvojicu viet opriamkach a rovinach na seba kolmych, która ma tu istu vlastnost.

Veta 16. Vsetky priamky kol-me na tu istu rovinu su navza-jom rovno beźne. Inymi slovami:

K royine existuje jeden koimy smer.

Yeta 17. Ysetky roviny kolme na tu istu priamku su navzajom rovno-beźne.

Yetu 16 a vetu 17 nebudeme dokazoyat.

Priklad 2. a) Dokażte, że existuje jedina priecka dvoch mimo-beżiek, która je kolma zaroveń na obidve priecky.

b) Zostrojte tuto priecku na kocke ABCDA'B'G'D' v zakladnej polohe, ak je BD' jedna a B'C' druha z obidvoch mimobeżiek. Urcte yzdialenost medzi priesecikmi priecky s mimobeżkami konstrukciou a yypoctom, ak je dane AB = a, AD = b, AA' = c.    w

Obr. 31

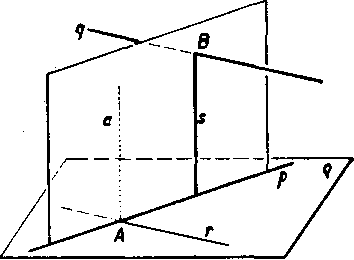
Rieśenie. a) (obr. 31.) Oznaćime p a q obidve mimobeżky. Na priamke p zvolime bod A a vedieme nim priamku r\\q. Ak existuje hladana priecka s, musi byt kolma na priamku pa r, te-da i na rovinu q = pr, lebo p a r su róznobeżky. K ro-vine q vsak existuje jediny koimy smer, a to smer a, kde a je kolmica na rovinu q v bodę A. Yśetky priamky smeru a, które pretinaju priamku p, su navzajom rovnobeżne a leżia v tejże rovine a=ap.

V tej to rovine teda musi le-żat hladana priecka s. Ak je B priesecik roviny <rs priam-kou q, musi hladana prieć-ka s prechadzat bodom B. Priecka s by neexistovala (lebo by existovalo nekonećne mnożstvo tyqhto priećok), keby priamka q a ro-vina a boli rovnobeżne. To vśak nie je możne, lebo potom by muselo platit aj r || a, co nie je pravda. Existuje teda vżdy jedina priecka s.

Miesto roviny a sme tież mohli poużit rovinu r, która je vytvorena priamkami smeru a, które pretinaju priamku q. Tak dójdeme k bodi> Csjua opaf k tejże priecke s.

b) Narysujeme kvader ABCDA’B'G'D' v zakladnej polohe (obr. 32). Nech p = BD' a } = B'C'. Za rovinu q z odseku a) zvolime royinu A'D'B a tym dostaneme smer a urceny priamkou B'H J_ A'B. Poużi-jeme druhu rovinu r z odseku a) a to je rovina G'B'H. Priesecnica rovin C'B'H a A'D'B je priamka HV || A'D'. Tym dostaneme bod V na priamke BD', którym ide hladana priecka s = VU.

Z obrazka vidiet, że VU = HB’, cim je konstrukciou dana skutocna vzdialenost obidvoch priesećikoy U a V. Eahkym yypoctom potom ac

^vypiyv_a UV = j7===.

ya² -f ^c2

175