1954 Geometria 216

jednu stranu riadiaceho mnohouholnika, tyoria stenu hranoloyej, płochy. Steny su pasy rovin a je ich zrejme prave tolko ako hran.

Veta 34. Hranołoyy w-boky priestor je utvar społoćny n polpriesto-rom, z których każdy je oddeleny jednouz rovin obsahujucich stenu pri-sluSnej hranolovej płochy a je urćeny l’ubovornym ynutornym bodom riadiaceho mnohouholnika.

Vetu 34 nebudeme dokazovat. Ilustraciu jej obsahu podava obr. 70 (pre n = 5).

Priamky smeru p volame yrcholoye priamky. Su dvojakeho druhu: Vrcholove priamky, których yśetky body patria hranoloyemu prie-

storu, alebo vrcholove priamky, których nijaky bod nepatri tomuto priestoru. Pri vrchołovych priamkach pryeho druhu móżeme este roz-lisovaf, ci patria vmitru hranolovćho priestoru alebo hranolovej płoche.

Roviny rovnobeżne so smerom p nazy vame vrcholove roviny.

Vrcholova royina ma s hranoloyou plochou spoloćnu bud! nekonecnu mnożinu vrcholovych priamok, ak obsahuje niektoru stenu, bud dve rożne vrcholove priamky, bud’ jednu vrcholovu priamku, a to hraiiu, bud’ nema s hranolovou plochou nijaky społoćny utvar (obr. 71a, b, c).

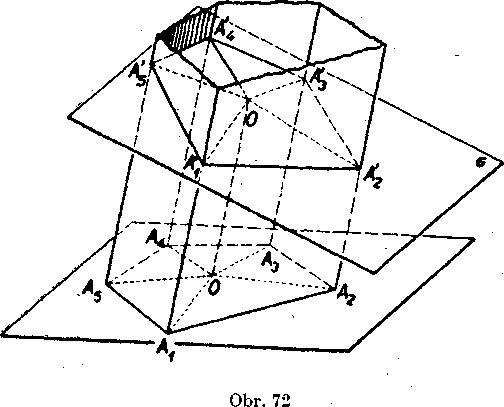
Rovina a, która nie je yrcholova, ma s hranoloyym n-bokym prie-storom społoćny yypukly n-uholnik (tzy. priesek royiny a hranoloyeho priestoru obr. 72).

Dokażeme dalsiu dóleżitu poućku.

Veta 35. Prieseky dvoch roraobeźnych, nie vrcholovych rovin a a t s hranolovym priestorom su zhodne mnobouholniky.

Dokaż (obr. 73). Oznacme a, r dane dve roviny; ak je a s r, je veta zrejma. Predpókladajme teda, że a & r. Oznacme B₁B₂. . ,B_n mnoho-uholnik, który je priesekom hranoloveho priestoru s rovinou a, a

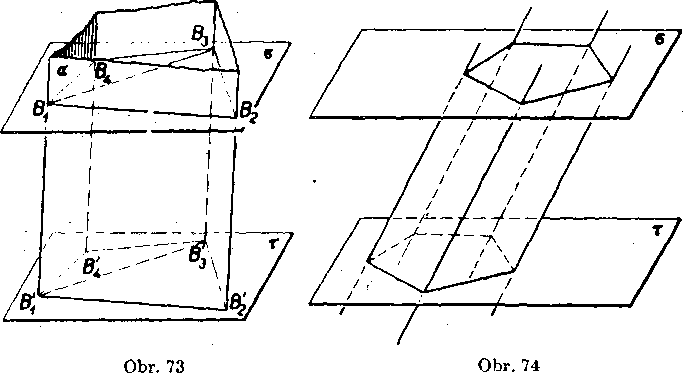
B{B₂... B'_n mnohouholnik, który je priesekom hranoloveho priestoru s rovinou r. Ożnaćenie śme zvolili tak, że body B_v B[, dalej body B₂, B₂ atd. leżia vżdy na tej istej hrane.

Podia vety 3 je B_tB₂ ||J3JB£, B₂B₃\\B'₂B!_S, B,_iB₁ \\B^B[. Pretoże je aj B_xB[ jI B.t.B^ |j B₃B₃, su obrazce B₁B₂B₂B{, B_żB₃B!_aB'₂, B.J\B[B_a rovnobeżniky, t. j. plati B_XB_Z = B[B₂, B₂B₃ = B’₂B₃, B₃B_X = B₃B[. Podia vety sss e teda

'A B_xBJB_z A A B[B₂Bi

Podobne móżeme dokazat, że plati

A B₁ĄB_i A A B[B’₂,Bl..., a B_xBJB_n A A B[B’₂Bi

Rovinu q premiestime tak, aby bod B[ presiel do bodu B_v bod B₂ do bodu B₂ a bod B₃ do bodu B₃; to je możne s jedinym yysledkom podia axiómy VIIIa. Pd tomto premiesteni prejde aj bod B_i do bodu B_x,. .., bod B_n do bodu B'_n, pretoże vieme, że napr. A B₁B₂B_i A A A B^BnB^, okrem toho bod B_i leżi v polrovine B₁B₂B_z a bod B^

217