1954 Geometria 286

imit nezavisi od, tołio, od której lomenej ciary vyjdome a a kym sposobom zvyśujeme pocet ich vrcholov, len nech sa splni podmienka, że sa dlżka jej najvacśej strany bliżi k nule. Tento limit nam po tom defi-

nuje dlżku obluka AB.

Popisanym sposobom sa v matematike skutocne definuje a pocita dlżka obluka krivky. Vśimnime si eśte, że tymto sposobom możno urcit aj dlżku usecky. Ak si totiż vo ynutri usecky AB zvolime v tomto poradi body 0„ O,,. .., C„_₁(obr. 42, kde n == 8), siicet dlżok

AC, + 0,0,+ ... C_n-, C_n +C_nB    (1)

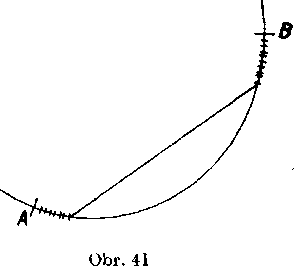
rovna sa dlżke usecky AB pre każde n. Ak neobmedzene zvacsuje-me n a pre każde n urcime sucet (1), dostaneme postupnost

AB, AB, AB, ,..., AB,.. .,

-I—I—H—I—f—

Obr. 42

której vsetky cleny rovnaju sa AB a aj jeho limit sa rovna AB.

II. Uved’me eśte druhy spósob, którym możno rozśirit pojem dlżky. Tymto sposobom budeme sa podrobnejśie zaoborat’.

Ak rysujeme usecku ceruzou, dostaneme pribliżne taky obrazec, aky vidime na obr. 43. Jednotlive kruhy predstavuju stopy hrotu

4    B

i 0 Q Q Q -O-d)

Obr. 43

pohybujucej sa ceruzky, pretoże hrot oeruzky nie je bod, ale mała plośka, której stopu móżeme povażovat za kruh o vel mi malom polo-mere q.

Ak nechceme pri opisovani utvaru z obr. 43 poużif slovo „pohybo-vat sa“, móżeme ho oharakterizovat takto: utvar na obr. 43 składa sa z bodov vsetkyeb kruhov o polomere o, których stredy su body usecky AB. Tento utvar vSak możno zlożif aj z obdlżnika MNPQ s rozmerm i AB. 2g a z dvoch polkruhov o polomere g (obr. 44). Podia kapitoly 2 (str. 270) je to obrazec, ktoreho obsah vieme urcit.

Ak tento obsah oznacime P_e,

P_s = 2 g.AB + tiq².

Keby sme obsah obdlżnika MNPQ delili jeho jednym rozmerom 2g, dostali by sme podiel, który sa rovna druhemu rozmeru, t. j. dtź ke

9    P

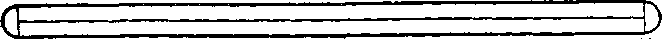
Obr. 44

usecky AB. Ak ćislom 2g delime obsah P_Q celeho utvaru, dostaneme podiel, który oznacime d_e:

d_a

P.

2 e

AB +

71

Q.

Podiel d_e odlisuje sa od dlżky usecky AB kladnym cislom — g. Tento podiel je pravdepodobne tym inenśi, cim menśi je polomer o.

1. Namiesto jedneho polomeru g zvo!me si postupnost polomero v {?!> (?2’ 93’ (?4> ■••>(?»>•••    (2)

tak, aby boi każdy nasledujuci clen tej to postupnost! pokmcou pred -ohadzajuceho clena (obr. 45), t. j.

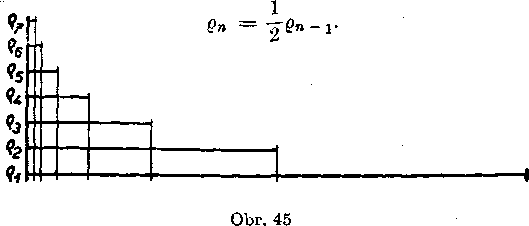
287