1954 Geometria 068

Ak mamę urcit yelkost duteho uh!a <£ A VB, nanaśame postupne jednotkovy uhol od polpriamky YA do polroviny VAB. Takto dosta-vame polpriamky VI\, VP₂, ... (obr. 81). Ak niektóra z polpriamok yP_n spłynie s ramenom VB, je vel'kost uhla AVB n jednotkovych uhlov. Ak je napr. jednotkovy uhol stupeń a ak spłynie polpriamka YP_Vi s polpriamkou VB, je yelkost uhla <yAVB 12 stupńov; zapi-srijeme to

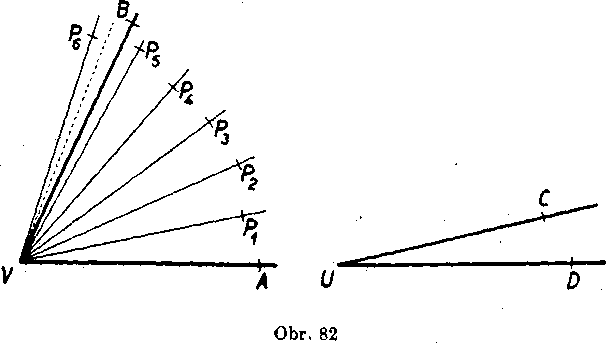
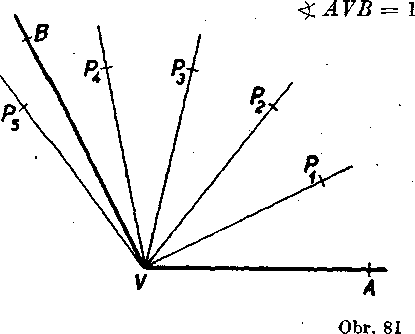
Óbycajne vśak nastanę pripad, który je znazornehy na obr. 82. Tu leid polpriamka VB vo ynutri uhla <£ P_nVP_n+1 (n = 5); meranim sine teda nezistili yelkost uhla <£A VB. Tak ako pri merani usećky, gó tu dve możnosti:

1.    Jednotkoyy uhol CUD możno rozdelit na urcity pocet zhod-nych casti, napr. na q casti tak, że ak zvolime jednu z tychto casti za novy jednotkoyy uhol, je yelkost uhla <£ AVB prirodzene cislo p. (Na obr. 82 je q == 3, p — 16.) V tomto pripade sa yelkost uhla <£A VB

pri jednotlcovom uhłe <£ CUD rovna raeionalnemu ci siu — (na

obr. 82 je yelkost-^).

ó

2.    Może sa ysak stat, że uhol <£ CUD nemożno rozdelit nijakym sposobom na zhodne casti tak, aby nastał pripad 1. To znamena., że yelkost uhla <£ AVB pri jednotkoyom uhle <£ CUD nemożno vy-jadrit nijakym raeionalnym (a teda ani nie celym) cislom. Potom hoyo-rime — podobne ako pri usećkach—że uhol AVB je nezmeratelny s uhlom <£ CUD.

Nebudeme dokazovat existenciu nezmeratelnych uhlov a ani nebu-deme bliżśie skumat tento pripad. Uvedieme iba, że yelkost uhla je v tomto pripade yyjadrena iracionalnym cislom.

Medzi dutymi uhlami ma yyznacne postavenie pravy uhol. Preto za jednotkoyy uhol volime spravidla urcitu ćast praveho uhla (napr. jedna devatdesiatina praveho uhla je jeden uhlovy stupeh). Ak je jednotkoyy uhol zvoleny tak, że yelkost praveho uhla je kladne cislo B, móżeme yyslovit zakladnu vetu o merani uhlov takto:

Każdy uhol (duty, priamy alebo yypukly) ma za yelkost’ kladne cislo mengie neż 4it. Obratene każde kladne Cislo mensie neż 4R je vel’kosfou urCiteho uhla (duteho, priameho alebo yypukleho). Zhodne uhly maju roynake yelkosti, a obratene: uhly, których yelkosti su roynake, su zhodne.

Tuto vetu nebudeme odóvodnovat, ale objasnime ju na prikladoch.

Priklad 1. Aku vel’kost ma pravy uhol, ak je jednotkoyy uhol c = 67° 30'?

Riesenie. Poużijeme obdobnu yetu, aku sme poużivali pri merani useciek:

Ak zmenime jednotkoyy uhol, nasobia sa vel’kosti yśetkych uhlov tym istym koeficientom, zvanym menitel’.

V naśom pripade ma pri jednotkoyom uhle ,,stupni“ prvy uhol vel’-kost 67,5, druhy 90. Ak zvolime prvy uhol za jcdnotkoy^, budę mat druhy uhol vel'kost-a; a podia uvedenej yety budę platit

90 : 67,5 = x : 1.

—    4

Z toho dostaneme x = 1,3 = —.

O

69