1954 Geometria 262

Ak oznaeime yelkosf strany CB plsmenom a a yelkosf useciek

CNX, CN2,	..., CNn^1 pismenami x1> x2, ..	xn^1, dostaneme
Pi	*0 j J. 2 A.J J. j *t,g	Pn-l ^n-l
P	a^2’ P a^2’ P a^3’	P a^2 ‘

X.

! _ 1

a* n a^c n a^c

n

n

a z toho

^Xi=]/i^a2; *²⁼⁼]/l^a2; -;^a:»-i = ]/-

Ak napiśeme napr.

7t

%-yeo-

vidime, źe je yelkosf odvesny pravouhleho trojuholmka, ktoreho

prepona ma dlżku a a prilahly usek prepony ma dlżku — a. Tak mó-

żeme zostrojif bod Ay (obr. 17) a podobne aj body N₂, A^r3, A^rn_₁. Konśtrukcia je na obr. 17.

Cvićenie

1. Je dany sedemuholmk ABCDEFG a usećka a. Zostrojte sedem-uholnik A'B'C’D'E'F'G' podobny danemu sedemuhołmku, ktoreho strana A'B' ma yelkosf a(a yŁ AB).

2. Dokażte, że obsahy dvoch trojuholnikoy, które sa zhoduju v jednom uhłe, su v rovnakom pomere ako sućiny veIkostł stran zvierajucich ten to uhol.

Odvod’te yzorec pre obsalr lichobeźnika tym, źe predlżenim ramien doplnite tento lichobeźnik na trojuholnik.

4. V akom pomere su obsahy lichobeźnika a trojuholmka v cyiceni 3?

P    NR

5.    Je dany lichobeźnik ABCD. Zostrojte priamku rovnobeźnu so za-kladńami tohto lichobeźnika tak, aby ho rozdelila na dve casti o rovnakom obsahu.

6.    Zostrojte podobne ako v cviceni 5 priamku tak, aby rozdelila dany lichobeźnik na dve casti s pomerom obsahov 2:1.

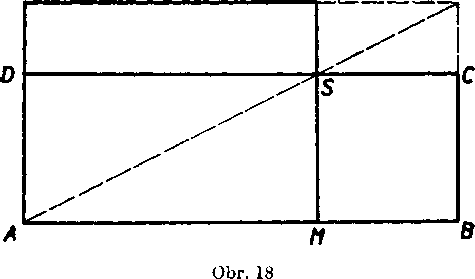
7.    Dokaźte, źe pravouhle stvoruholniky ABCD, AMNP na obr. 18 maju ten isty obsah.

3. VeIkosf strany pravide!neho n-uholmka Obsah pravidelneho n-uholnika

Pravidelnymi w-uholnikmi ste sa zaoberali uź v 10. rocniku. Naucili ste sa, źe każdy pravidelny n-uholnik możno zlożif z n zhodnych rov-noramennych trojuholnikov, których zakladna je stranou pravidel-neho w-uholnika (yelkosf strany prayidelneho 7i-uholnika móżeme oznacovaf a_n). Ramena tychto trojuholnikoy su polomery krużnice opisanej n-uholniku a yysky tychto trojuholnikoy su polomery kruż-

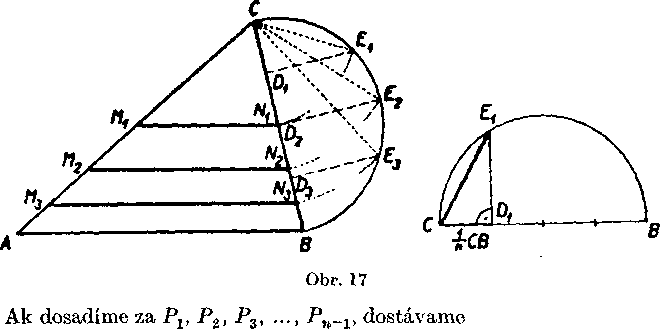
x

263