1954 Geometria 074

że jeho strany su v pomere 1 : ]/'3 : 2. To znaci, że ak ma kratśia od-vesna (oproti uhlu 30°) yelkosf 1, ma dlhśia odyesna (oproti uhlu 60°) yelkosf ]/3. Preto

^tg3°°=P = ^ tg 60°= & = ]/3.

Pretoże każdemu kladnemu eislu oc < 90 je priradene jedine kladne ćislo tg a,tvori toto priradenie funkciu, ktoru nazyyame funkcia tan-gens, tak, ako napr. funkciu y — 2 r nazyyame priama umernosf. Ćislo tg a sa nazyya hodnotou funkcie tangens.

Na obr. 87 su zostrojene dva pravouhle trojuholniky ABX, ABY, których odvesna AB ma yelkosf 1 (deeimeter). Ak yyjadrime yelkosti useciek BX, BY v decimetroch, dostaneme tg<£XAB, tg<£YAB. Skutocne je

tg <£XAB =

BX

AB

BX

1

= BX

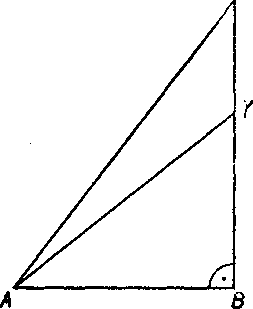
Obr. 87

a podobne

t g-źYAB^-j^ =

Pretoze je <£ XAB > <C YAB, je podia znamej vety z planimetrie aj BX >BY.

Z tejto ńyahy vyplyva yysledok :

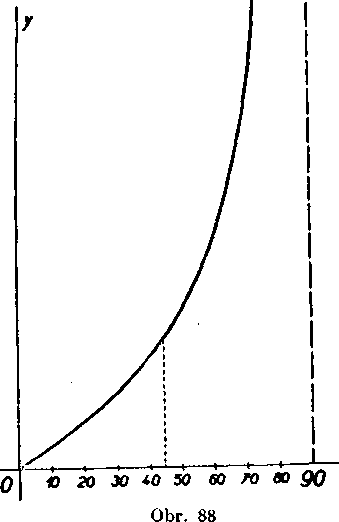
1. Ak yzrastó yelkosf ostreho uhla, yzrasta prislusna hodnota tangens. Ina? yyjadrene: ak je <x > /l, je tg a > tg fi.

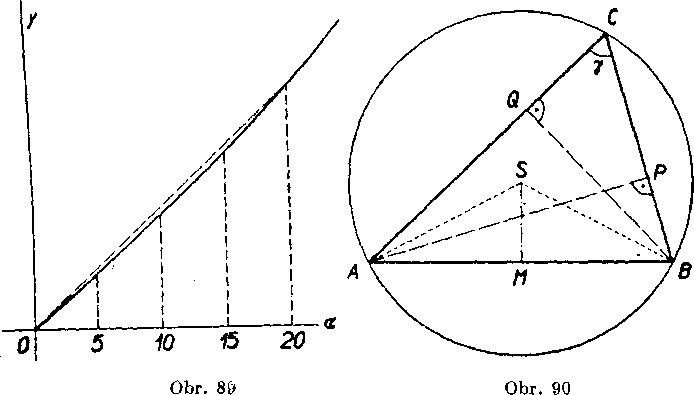
Odvesnu BX móżeme zvolit tak, że jej vel’kosf (v dm) budę sa rovnaf 1’uboyornemu kladnemu cislu. Z toho vyplyva:

2. Funkcia tangens nadobuda ysetky kladne hodnoty.

Priklad 5. Medzi yelkosfami uhlov 0°, 30°, 45°, 60°, 90° marne najsf

2

medza pre uhly a, fi, pre które plati tg a — —, tg fi = 2,7.

U

Rieżenie. Vieme, że

t_g 30° ^ li == 0,577, tg 45° = 1, tg 60° = ]/3 = 1,732. Pretoze je 3

75