1954 Geometria 200

Cyicenie

1.    Dokażte, że utvar zlożeny z troch rovin, z których każde dve su na sebe koime, ma 9 rovin sumernosti.

2.    Dokażte, że IubovoIne dve priamky, dva smery, dve polroviny a polpriamky su utvary zhodne.

3.    a) Je dany stvorsten ABGD a bod E ^ D tak, że AD = AE,

BD = BE, CD = CE. Dokażte, że rovina ABC je rovinou sli-mernosti usecky DE.

b) Poużitim yysledku a) dokażte, że dva śtvorsteny ABCD a A'B'C'D', pre które plati AB = A'B', BC = B'C, C,A = CA' AD = A'D', BD = B'D’, CD = C'D', su zhodne. -i.

4.    Dokażte że dva trojuholniky ABC a A'B’C', pre które plati AB = = A'B’, AC = A'C, BC = B'C, su priamo zhodne podia defi-nicie zhodnosti priestoroyych utvarov.

5.    Dokażte, że każde dve kocky o tejże dlźke hrany su priamo zhodne.

6.    Uved’te niektóre hudobne nastroje, które by sa mohli poużit (pre normalne cvićeneho hudobnika) v nepriamo zhodnej podobe.

7.    Popiśte zhodne zobrazenie, które vznikne zlożenim dvoch rovino-vych sumernosti, których royiny sumernosti su na seba koime.

6. Odchyłka dvoch priamok, odchyłka priamky od royiny, odchyłka

dvoch rovin

V planimetrii sme zaviedli uhol duty, priamy a yypukly a każdemu z tychto uhlov sme priradili kladne cislo, nazyyane vel’kost uhla.

Yelkost uhla yystihuje ciselne, ako sa napr. urćita priamka v rovine odchyluje od priamky s ńou róznobeżnej. Pojem vel’kosti uhla roz-sirirne teraz tak, aby sa vztahoval aj na utvary v priestore, napr. na dve mimobeżne priamky.

Definicia. Nech su dane dva smery a, b. ZvoIme IubovoIny bod X v priestore a ved’me nim priamku a' smeru o a priamku b' smeru b. Odchyłka to smeroy a, b je cislo, które urćime takto:

a)    Ak splynu priamky a', b', je co = 0.

b)    Ak su priamky a', b' róznobeżne, je co yelkost ktorehokolyek ostreho alebo praveho uhla, zovreneho priamkami a', b'.

Poznamka. Aby mała vyslovena definicia zmysel, musime si uve-domit, że cislo nezavisi od yolby pomocneho bodu X.

Skutocne, ak su obidva smery a, b totożne, plati pre każdy bod X yztah a' = b', a teda to = 0.

Ak su smery a, b różne, su priamky a', b’ róznobeżne a yelkost co je podia vety 12 pre każdy bod X ta ista.

Predośłu definiciu doplnime takto:

Odchyłka dvoch priamok a, b (rovnobeżnych, róznobeżnych alebo mimobeżnych) je odchyłka smerov a, b.

Podia vyslovenej definicie je zrejme, że napr. odchyłka kolmych priamok je 90°, odchyłka rovnobeźnych priamok je 0°.

Pre strucnost zavedieme eśte tento zapis: odchyłku priamok p, q (smerov p, q) budeme zapisovat znakom <£ pq («£ p q).

Vyslovlme teraz dalśiu definiciu.

Definicia odchylky priamky od royiny. Ak je priamka p kolma na q, hoyorime, że odchyłka priamky p od royiny q je 90°. Ak nie je priamka p kolma na rovinu o a ak je p₀ pravouhly priemet priamky p do roviny q, nazyvame odchylkou priamky p od roviny q odchyłku priamok P> Po-

Odchyłku priamky p od roviny budeme zapisovat znakom pę.

Veta 30. Nech je p priamka a q rovina. Odchyłka priamky p od kto-rejkoIvek priamky roviny g je vac§ia neź odchyłka <£ pg, alebo sa jej rovna.

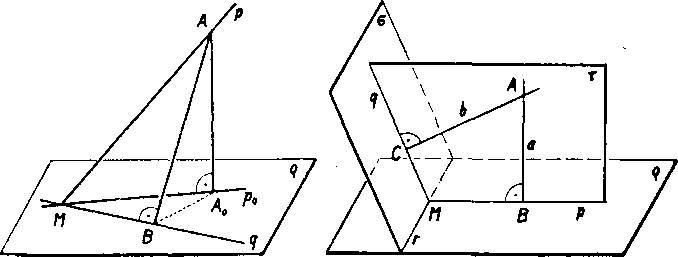
Obr. 50    Obr. 51

Dokaż (obr. 50). Ak je p || g, je veta jasna, lebo potom ^f.pg = 0. Możno teda predpokladai, że existuje priesećik M = p.g. Ak je p J_ J_ g, rovnako netreba nic dokazovat, lebo potom    = 90°,

'ź'pg rovna sa <Ppq, kde q je IubovoIna priamka v g.

Predpokladajme teda, że nie je p J_ g; potom existuje priamka p₀ ako pravouhly priemet priamky p do roviny g. Oznaćme A * M bod na priamke p a A₀ jeho pravouhly priemet do roviny g. Za lubo-

201