1954 Geometria 008

= AB a bod M, który neleŻi na priamke KL. Potom dany utvar możno preniiestif s jedinym vysledkom tak, aby bod A preSiel do bodu K, bod B do bodu L a bod C do urSiteho bodu C' polróviny KLM. Pri tomto pre-miesteni prejde każda usecka v usecku s ńou zhodnu a każdy uhol v uhol s nim zhodny.

Poucku (5) móżeme vyskmt takto: K rovinnemu utvaru, który nie je castou priamky, możno zostrojit jediny zhodny xitvar, który vyho-vuje podmienkam, vyslovenym vo vete (5).

Podia poucky (5) móżeme zostrojit k danemu uhlu Ul A YB jediny s nim zhodny uhol <£ CUD, ak je vopred dana polpriamka UG a pol-rovina UCD. Zostrojenie uhla <f- GUD sa nazyva prenesenim uhla < AVB k polpriamke UG do polroviny UGD (obr. 13). Prenaśanie uhlov nam umożńuje uhly zrovnavat, graficky scitat a odcitaf.

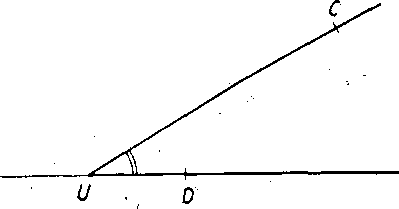
Obr. 13

O zhodnost uhlov opiera sa pojem pxaveho uhla. Dhty uhol sa na-zyva pravy, ak je zhodny s niektórym svojim vedlajsim uhlom. Dve róznobeżne priamky urćuju (niekedy hovorlme ,,zvieraju“) śtyri dute uhly; ak je jeden z nich pravy, su prave aj vśetky tri zvyśne a priamky su navzajom kolme.

Każde dva prave uhly su navzajom zhodnó; preto móżeme rysovat kolmice podia jedneho urćiteho praveho uhla — trojuholmkoveho pravitka. Preto tież poużivame pravy uhol alebo jeho ćast (stupeń) na.meranio a na porovnavanie uhłov. Ak je duty uhol mensi neż pravy, hovorime, że je ostry, a ak je vaesi neż pravy, hovórime, że je tupy.

O zhodnost uhlov opiera sa aj pojem osi uhla. Os duteho alebo pria-meho uhla A VB je polpriamka VG, która prislucha tomuto uhlu a dęli ho na dve zhodne casti Ul A VG = Ul BVG.

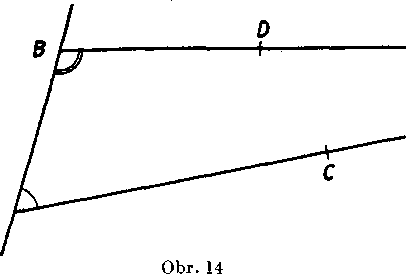
Uhly m ABD a m BAG, które leżia v tej istej polrovine, oddaleń ej priamkou AB (obr. 14), volaju sa prilahle.

Ak je sucet prilahlych uhlov priamy, su priamky AG, BD rovno-biżne; obratene,*ak su priamky AG, BD rovnobeżne, je sueetprilah-lych uhlov ABD a BAG uhol priamy.    ’ e .

Tieto poucky pouźivame vel’mi ciasto pri żistovam, ći su dve priamky rovnobeżne, a o ne sa opiera aj rysocanie rovnobeżiek pomocou dvoch trojuholnikovych pravitok.

Zpoucky(5) sa odvo-dzuju tzv. vety o zhod-nosti trojuholmkoy. Su to śtyri poucky, ozna-ćovane skratkami: sus, usu, sss a Ssu. Tieto poucky nam umożnuju zistit zhodnost dvoch trojuholnikov na żaki ade zhodnosti nie- ą których dvojic stran a uhlov. Z viet o zhodnosti trojuho!nikov vy-ply va cely rad różnych vlastnosti. Niektóre z nich zopakujete vo cvićeniach.

Cvicenie

1.    Narysujte Iuboyolny trojuholnik ABC, urcte graficky polovicu p jeho obvodu a zostrojte usecky p — AB, p — BC, p — GA. Aku usecku da sucet prvych dvoch z nich 1

2.    Zostrojte euklidovsky stred usecky, rozdelte usecku na 5 zhodnych casti. Zostrojte euklidovsky os uhla,

3.    Narysujte róznostranny trojuholnik, zostrojte jeho vyśku, os uhla a tażnicu yyehadzajlicu z toho isteho vrchołu. Porovnajte ich medzi śebou a yysledok zapiśte.

4.    Obr. 15. Bod X leżi vo vnutri /\ ABG. Dokażte, że AX Ą- BX < < A (■ 1- BC. Navód: Poużite vety o sucte dvoch stran trój uholnika na A ,107 a Ą KXY. ,

5.    ABCDEF je praridelny Sestuholnik. Naneste usecku BF na pol-priamku DC-, dostanete bod G. Premiestite śestuholnik tak, aby body B, F preSli po rade do bodov D, G a aby sa bod A premiestil do polroviny DCB.

6.    Zostrojte IubovoIny trojuholnik ABC a opiśte mu krużnicu k. Na obluku AB, na ktorom neleżi bod C, zvo!te si bod D. Graficky scitajte uhly ,<^ ACB, X ADB a presyedcte sa, żę ich sucet je uhol priamy, J

9