1954 Geometria 004

Priamka je rozdelena każdym svojim bodom na dve polpriamky, zvane opacne. Polpriamka PA obsahnje body P, A a vśetky take body priamky PA, które nie su oddelene od bodu A bodom P (obr. 1). Opacne polpriamky PA, PB maju spolocny iba zaćiatok P.

llsećka AB je spoloćnou ćastou polpriamok AB, BA. Useeka AB obsahuje jednak svoje krajne body A, B, jednak vśetky body X priamky AB, które oddeluju body A, B, alebo body, które leżia medzi bodmi A, B.

Rovina je rozdelena każdou svojou priamkou na dve polroyiny, zvane opacne. Polrovina pA obsahuje bod A, vsetky body priamky p a YŚetky take body roviny, które nie su oddelene od bodu A priamkou p (obr. 2). Opacne polroviny pA, pB maju spoloenu iba hranićnu priamku p.

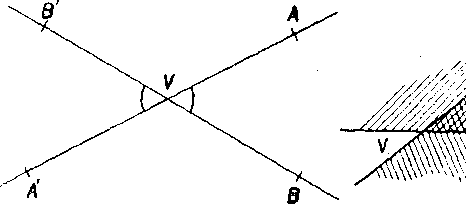
Dve różne polpriamky VA, VB, które maju ten isty zaćiatok, delia rovinu na dve casti, zvane uhly. Ak su polpriamky VA, VB opacne (obr. 3), je każda z obidvoch casti polrovinou a nazyvame ju uhol priamy. Ak nie su obidve polpriamky VA, VB opacne, neleżia body A, B, V v priamke. Potom jedna casi roviny, obmedzena polpriam-kami VA, VB sa składa zo vśetkych polpriamok VX, kde je X l’ubo-vo!ny bod usećky AB (obr. 4); tato casf sa vola duty uhol AVB a zapisuje sa AFR. Druhy uhol, obmedzeny polpriamkami VA, VB sa vola yypukly. Pre vypukly a priamy uhol nepoużivame znak A-K uhlu A VB (ci je duty, priamy alebo vypukly) patria i jeho ramena VA, VB, a teda aj jeho vrchol V.

Duty uhol A AVB je spolocna casi polrovin VAB, VBA (obr. 5). Spolocna. casi opacnych polrovln VA'B' a VB'A' je duty uhol A A'V'B' (obr. 6), który je k danemu uhlu vrpholovy. Uhly A AⁱVB a A B'VA su uhly vedlaj§ie k uhlu A- AVB.

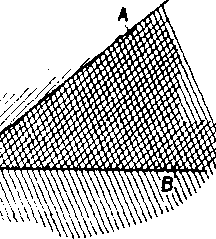
Tri body A , B, C, które neleżia na jednej priamke, urcuju tri usecky AB, BC, CA, które teoria obvod trojuholnika ABC. Trojuholnik ABC¹

je spolocna cast polrovin ABC. BCA a CAB (obr. 7), obvod je castou

Obr. 5    Obr. 6

%

trojuholnika. Dute uhly <£ CAB, <y ABC, A BCA sa eolaju ynutorne uhly trojuholnika; ich redlajsie uhly su ronkajsic uhly trojuholnika. Trojuholnik je casfou każdeho svojho ynutorneho uhla.

Obr. 7    Obr. 8

Ceicenie

1. V rovine je danych sest różnych priamok a_v a₂, a₃, a_ą, <z₅, a₆. Plati ^ai !!    || «4- 0.5 |! «₆; inac su każde dve róznobeżne. Priamky a₁. a₃,

a_s prechadzaju jednym bodom. Inac nijake tri z danych priamok neprechadzaju tym istym bodom. Naćrtnite sesfc takychto priamok a zistite, kolko priesecikoy yznikne.

5