1954 Geometria 148

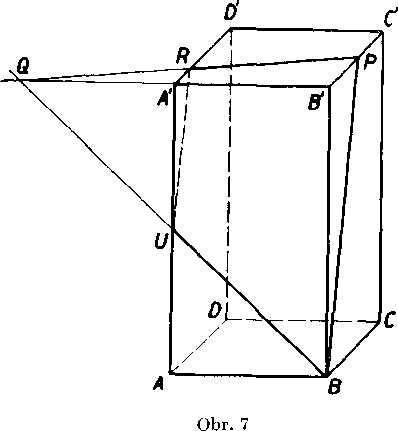
A'B’0* je priamka PQ, priesecnica rovm A'B'C', ADD' je priamka, A'D'\ preto je bod R priesecikom priamok PQ, A'D'. Obdobne zo-strojime priesecik priamok BQ, AA', t. j. bod U.

Priesek daneho kvadra s rovinou BPQ je śtvoruholnik BP RU. Możno dokazat’, że BPRU je śtvoruholnik, v ktorom je BP |j RU, naproti tomu nie je RP\\BU. O rovnobeżnosti priamok BP, RT sa móżeme presvedcit z obrazka vzhIadom na to, że plati ylastnosf (b).

B. K druhemu sposobu rieśenia konsularnych uloh. Pri postup-nom rysovani rovinnych konstrukcii predpokladame, że każda rovina, v której robinie niektoru konśtrukciu, je jednoznacne urcena niektórym z tychto spósobov:

a)    su dane tri jej body neleżiace v priamke;

b)    je dana jej priamka a jej bod neleżiaci na tej to priamke;

c)    su dane dve jej róznobeżky;

d)    su dane dve jej nesplyvajuce rovnobeżky.

Priklad 3. Marne narysovat liohobeżnik PRUB z prikladu 1 v sku-tocnom tvare a vel’kosti.

Riesenie. Pre 1’ahsiu orientaciu poużijeme obraz vo vo!nej projek-cii (obr. 7). Postup rieśenia budę tento:

V    rovine BCC' zostrojime obdlżnik BCC'B' a usecku BP v skutoc-nej vel’kosti (obr. 8a).

V    rovine A'B’C' zostrojime obdlżnik A'B'C'D', body P,Q a usecku PQ v skutocnej vel’kosti (obr. 8b).

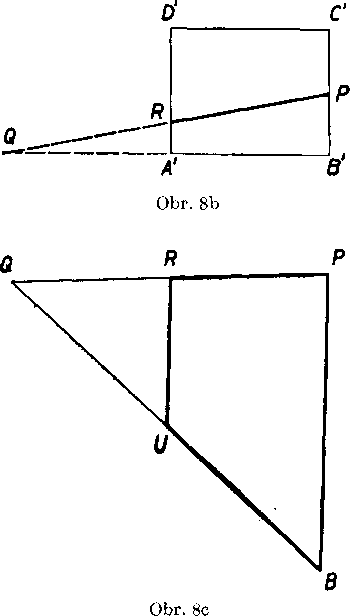
Pretoże na obrazę vo vol’nej projekcii je podia ylastnosti (a) usecka BQ v skutocnej vel’kosti, zostrojime v rovine PQB trojuholnik PQB (obr. 8c). Aj usecka BU je. na obr. 7 v skutocnej veIkosti a dalej ]eRU\\BP, cim dostaneme na obr. 8c lichobeżnik PR UB v skutocnej ve!kosti.

Pri rieśeni konśtruk-cnej ulohy v priestore postupujeme rovnako ako pri rieśeni konśtrukcnej ulohy v rovine: najskór urobime rozbor ulohy, z neho vyplynie konśtruk-eia, ktoru potom, pravda, treba dokazat; napokon urobime diskusiu, v której zistujerne najma podmień-ky rieśitelnosti.

Priockou dvoch mimo-beźiek nazyvame priam-ku, która je s oboma róznobeżna. Rozrieśime nasledujucu ulohu o priec-ke dvoch mimobeżiek.

Priklad 4. Je danv kvader ABGDA'B'C'D' v zakladnej polohe. Bodom B vedieme v rovine ABC priamku p. która je mimobeżna s priamkou q = AC'. Marne zostrojit priećku r mimobeżiek p, q, prechadzajucu bodom A' a zistit vzdialenost oboch priesećikov priamky r s obidvoma mimobeżkami P, 2-

Rieśenie. a) Rozbor (obr. 9). Ak existujehl'adanaprieckar,pre-phddza bodom A' a leżi v rovine 4'? s A'AC', Tato rorina neobsa-

149