1954 Geometria 132

Obraz zaciatku je zaciatok; teda obraz każdeho bodu paraboly (1) je bodom paraboly (2). R.ovnako możno odóvodni£, że każdy bod paraboly (2) je obrazom niektoreho bodu paraboly (1), a tym sme naśe tvrdenie dokazali.

^ Cvicenie

1.    a) Najdite podmienku, aby boli dva obdiżniky podobne.

b) Najdite podmienku, aby boli dva rovnobeżniky podobne.

2.    Dokaż te vetu: Ak su dva obluky krużnice podobne, su stredove uhly, które k nim prisluchaju, zhodne. Możno tuto vetu obratit?

3.    Narysujte IubovoIny śtvoruholnik ABCD a zvol’te tri body K, L, M' tak, aby neleżali na priamke. Zostrojte stvoruholnik A'B'C’D' podobny danemu tak, aby boli splnene tieto podmienky: 1 .A' = K; 2. B' leżi na polpriamke KL; 3. C' leżi v polrovine KLM\ 4. A'B' —

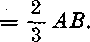
4. Ak je ABCD rovnobeżnik, su stredy jeho stran vrcholmi ineho rovnobeżnika. Dokażte: Ak je AC = AB.]/2, je tento rovnobeżnik podobny danemu. Navod: Poużite vysledok cvicenia lb) a cvicenia 8

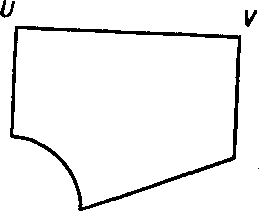
Obr. 152

z clanku III/3.

5.    Dokażte: Każde dva pravidelne śestuholniky su podobne.

6.    Obdiżniky ABCD a A'B'C'D’ su podobne a pritom je AC |j A'C. Dokażte, że su roynolahle.

7.    K utvaru na obr. 152 zostrojte u-tvar podobny tak, aby usecka UV presla do usecky U'V', która ma dvojnasobnu dlżku. Zmerajte sami potrebne dlźky a zostavte plan prace.

8.    Licbobeżniky ABCD, A’B'C'D' maju zakladne AB, A'B’. Su urćite podobne, ak je A'B' = Ic.AB, C'D' = Tc. CD, A'C' = k.AC? (Je je kladne cislo.) Navod: Zostrojte bod E na predlżeni usecky AB za bod A tak, aby EA = CD. Uvażujte o A EBD a o obdobne zostro-jenom A E'B'D'.

9.    Urcte podmienku, aby boli dve medzikrużia podobne.

5. Topograficke prace so stolikom

Prakticke poużitie rovno!alilosti je v pracach s meracskym stolikom. S meracskym stolikom ste sa oboznamili v 8. rocniku ą vykonavali ste s nim dve jednoduche prace: tzv. pretinanie vpred a rajónovanie.

Rajónovanie je v podstate zostrojenie rovno!ahleho trojuholnika k trojuholniku v terene na podklade vety sus. Aby sme vśak mohli

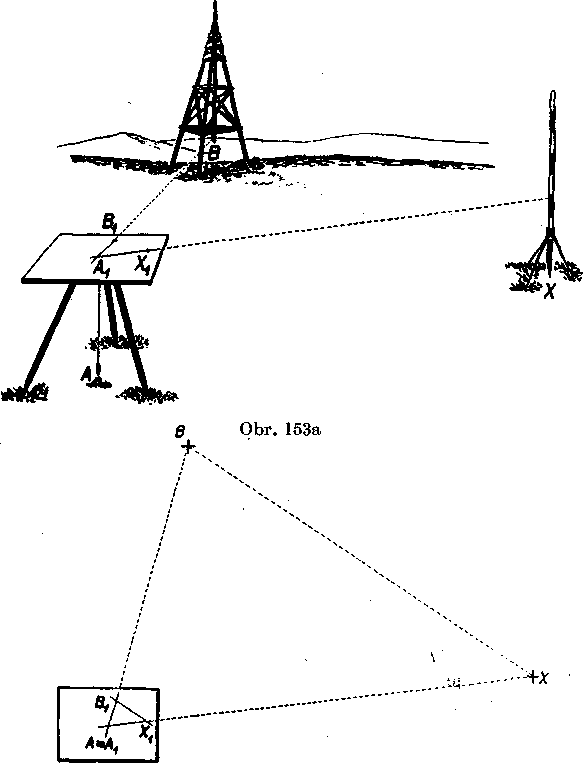
Obr. 153b

133