1954 Geometria 176

Ovićenie

1    Nech je ABCD rovnobeżnik o strede 0; mimo roviny rovnobeżnika "je dany bod V, o ktorom plati VA = VC, VB = VD. Dokażte, że OV J_ ABC.

2    Nech su dane priamky k || l || m, które neleżia v jednej rovine. Oznacme K IubovoIny bod priamky k a L, M paty kolmic KL, KM, yedenych bodom K na priamky l, m. Dokażte, że LM J_ l a LM J_ m.

;.T, Nech je dana rovina q a v nej bod R a dalej priamka q. Ved'te v ro-vine q bodom R priainku k Urobte diskusiu. Zobrazte ulohu na kvadri ABCDA'B'C’D' v zakladnej polohe. Vol’te R = C’, q = CDC', q = CA’.

?.,Ćo yyplnuju priamky kolme na darni priamku a preehadzajuce danym bodom ?

5.    ćo yyplnuju priamky kolme na danu royinu a pretinąjuce danu priamku 1 Urobte diskusiu.

6.    Su dane dve różne priamky pag. Dokażte, że ak możno priamkou p viesfi rovinu kolmu na q, możno priamkou q viesf rovinu kolmu na p. Kędy to nastanę? Aku polohu ma priesecnica obidvoch rovin k priamkam pag?

7. Dokażte: Existuje jediny koimy smer k dvom danym różnym smerom.

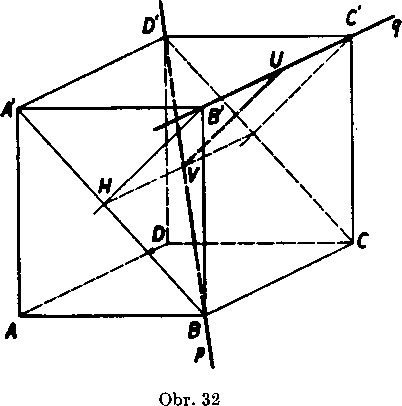
SL Je dany bod C' a dve priamky BA', AG. Bodom C' ved'me priamku k, która je kolma na priamku BA' a pretina priamku AC. Urcte podmienky riesitelnosti. Zobrazte na kyadri ABCDA'B'C'D' v za-kladnej polohe.

9. Rozhodnite, które z nasledujucich usudkoy su sprayne a które nie, a odóvodnite to: (a, b, c, p, q su priamky, n, q, a su roviny.)

a) Ak je p J_ q, q ]| a, je p _L a. b) Ak je pip, p\\ q, je q ± q. c) Ak je p    J_ Q,    ql    Q,    je p    |j    q.    d) Ak je p _L q,    p JL o, je    p || a.

e) Ak je a    J_ b,    b J_    c,    je a    ||    c.    f) Ak je a J_ b,    b J_ ^c> je    a _L c.

g) Ak je a    _L b,    b |l    c,    je a    c.    h) Ak je a J_ b,    b || rc, je a _[_ n.

i) Ak je a    _L Q,    b jj    q,    je a JL    b.    j) Ak je a J_ b,    6 1 n, je    a || n.

10.    Je dany śtvorsten ABCD; AB = BC = 5 cm, CA = 6 cm, AD — = BD == CD = 7 cm. Urcte patu E kolmice vedenej bodom D na rovinu ABC. Urcte useeky AE, BE, CE v skutocnej vel’kosti.

11.    Je dana kocka ABCDA’B'C'D' v zśikladne] polohe; stredom useeky AC je vedena rovina q 1_ AC.

a)    Vo vol'nej projekcii zobrazte priesecnicu rovin q, ACC a prie-secnicu rovxn q, ABC'.

b)    Zobrazte priesek roviny q s kockou.

2. Roviny navzajom kolme

Pojem roviny kolmej na inu danu rovinu zavedieme definiciou, która pre svoju jednoduchosfi slużi sucasne aj ako kriterium kolmosti dvoch rovin.

Definicia. Rovina a je kolma. na rovinu g (piseme a _L o), ak a obsahuje priamku kolmu na q.

Ihned zistime, że roviny kolme na danu rovinu skutocne existuju. K danej rovine existuje totiż cely smer kolmic. Ak si z nich jednu vy-berieme a ak zvolime mimo nej bod, je nim urcena royina, która je podia definicie kolma na danu rovinu.

V nasej definicii nie je vśak uspokojive to, że v nej obidve royiny neyystupuju rovnakym sposobom: v jednej z nich leżi priamka, która ma byt kolm4 na druhu rovinu, t. j. aspoń na dve róznobeżne priamky druhej royiny. Możno vśak dokazat, że aj v druhej rovine leżi priamka

177