1954 Geometria 180

Defini cia. Nech je dana rovina 71 a IubovoIny bod X. Ratu kolmice vedenej bodom X na rovinu n nazyvame prayouhlym priemetom bodu X do roviny n.

Nech je dana rovina n a IubovoIny geometricky utvar U, t. j. Iu-boYoIna mnożina bodov. Każdy bod utvaru U ma urcity pravouhly priemet do roviny tv, mnożina vsetkych tychto priemetov sa nazyva prayouhlym priemetom utvaru U do roviny n.

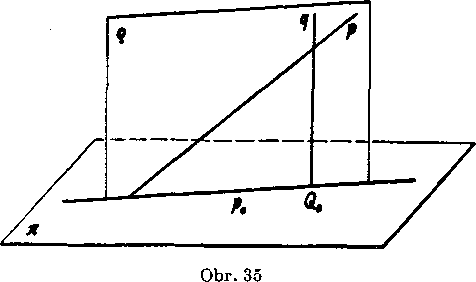
Podia tejto definicie je priamka p₀ = q.ti na obr. 35 pravouhlym priemetom priamky p do roviny n. Każda priamka, która nie je kolma na 7t, md teda jednoznacne urceny pravonhly priemet do tc a tymto priemetom je priamka p₀. Rovina a, pomocou której boi priemet p₀ urceny, vola sa premietacou rovinou priamky p do n pri pravouhlom premietani.

Ak je priamka p J_ 71, je podia definicie jej pravouhlym priemetom do Ti jediny bod, priesecik p₀ = p.71. Napr. na obr. 35 je bod Q₀ pravouhlym priemetom priamky q do n. Y tomto pripade nie je pre-mietacia rovina priamky q A. 71 urćena.

Veta 22. Je dana rovina n a priamka p, która nie je kolma na 71. Ysetky priamky y rovine 7t, które su kolme na priamku p, su kolmd na prayouhly priemet p₀ priamky p do roviny 71 a naopak.

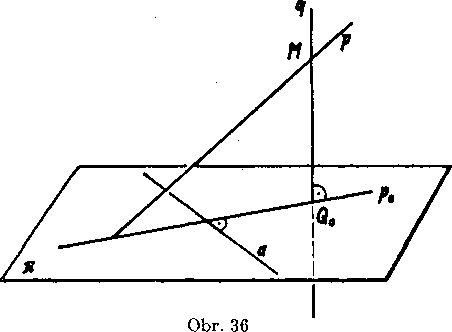
Dókaz (obr. 36). Z l’ubovol’neho bodu M priamky p vedieme kolmicu q _J_ 71. Każda priamka roviny 71 je kolma na priamku q. Ak je teda niektóra priamka a J_ P> potom je a J_ a, kde a = pq, a teda aj a J_ Po> pretoże priamka p₀ leżi v rovine a. Obratene, ak je a _|_ Po, je a A °, a teda a _|_ p-

Dósledkom vety 22 je dalśia veta, która sa velmi ćasto poużiva v rysovani.

Yeta 23. Su dane dva navzajom kolnie smery, z których jeden je rovnobeźny s rorinou n a druhy nie je na nu koimy. Prayouhle priemety do 7t IuboYolnych dvoch priamok, yzatych po jednej z kaźdeho smeru, su na seba kolme.

Dokaż. Oznacme p a q obidya smery a nech je p || n. Ak je a Iu-bovol’nou priamkou smeru p, je jej pravouhly priemet a do roviny n aj priamkou smeru p, ćo vyplyva z vety 5. Je teda a₀ J_ b, kde b je IubovoInou priamkou smeru q. Podia predchadzajucej yety plati a₀ J_ _L b₀, kde 6₀ je prayouhlym priemetom priamky b do n.

Priklad 3. Zistite, aky utvar je prayouhlym priemetom rovno-beżnika do royiny n.

Rieśenie. Ak je royina rovnobeżnika ABCD kolma na n, je prayouhlym priemetom każdej strany bud’ usecka, leżiaca na priesecnici rovin ABCD a n, bud' bod v tej to priamke. Priemetom roynobeżnika je v tomto pripade usecka. Ak nie je royina ABCD kolma na n, nie je nijaka strana roynobeżnika kolma na n a ysetky strany roynobeżnika maju za pravouhly priemet usecky, z których nijake dve nemóżu leżat v priamke. Priemetom je teda śtvoruhslnik A₀B₀C₀D₀ (obr. 37). Premietacie roviny ABB₀A₀ a CDD₀C₀ su rovnobeżne, lebo v ABB₀A₀ leżia dve róznobeżne priamky, które su rovnobeżne s CDD₀C₀, a to AB || CD a, AA₀ || CC₀ (kolmice na rovinu n). A preto A₀B₀ |] C₀D₀. Prave tak ukażeme, że B₀C₀ || A₀D₀, t. j. stvoruholnik A₀B₀C₀D₀ je rovnobeżnik. Roynobeżnik A₀B₀C₀D₀ budę obdlżnikom, ak budę ABCD obdlżnik, ktoreho royina nie je kolma .na n a ktoreho

181