1954 Geometria 206

yśetky mnohouholniky, którymi sa budeme zaoberat. Vyslovime de-finiciu.

Definicia. Nech je danych n trojuholnikoy OA_xA₂, /\OA₂A._a,

..., /\OA_n^_xA_n, AOA_nA₁ (obr. 57, kde n = 6), które maju tieto vlast-nosti:

1.    Nijake dva z nich sa neprekryvaju.

2.    Nijake tri zo susednych bodov A_X.A₂, ..., A_n neleżia na jednej priamke. Pritom susednymi bodmi nazyyame body, których indexy

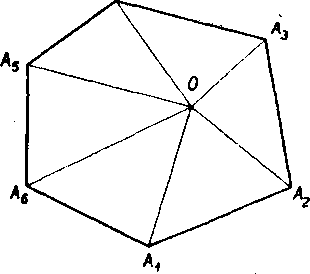
sa lisia o jednotku; napr. A_x, A₂, ale-bo A₄, A₅; aj body A_ń, A_x povażuje-me za susedne.

3. Priamka, która spaja dva l’u-bovol’ne susedne body, rozdeluje roviny na dve polroviny tak, że yset-ky body A_x, A₂,^4_naj bod O leżia v jednej z tychto polrovin.

Mnożinu vsetkych bodoy vśet-kych tychto trojuholnikoy nazy-yame Aypuklym mnohouholnikom A_xA₂...A_}j.¹)

Body A_x, A₂,..., A_n su yrcholy mnohouholnika, usecky A_XA₂, A_nA_x su strany mnohouholnika. Body stran tvoria obvod mnohouholnika.

i O bodoch mnohouholnika, które nie su bodmi obvodu, hoyorime, że leżia vo ynutri mnohouholnika. Vśetky ostatne body roviny leżia zvonku mnohouholnika.

Uhly fA_xA₂A₂, Ą:A₂A₂A₄, <C A_n___xA_nA_x, <r A_nA_xA₂ nazyyame ynutornymi uhlami mnohouholnika.

Poznamky. 1. Namiesto ,,mnohouholnik“ poyieme niekedy urcitej-śie ,,w-uholnik“ (n je prirodzene ćislo n A 3). Tymto sme poyedali, że mnohouholnik ma n vrcholov a n stran.

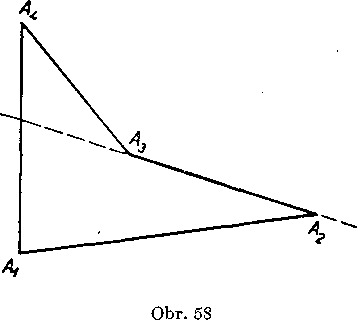
2. Keby nebola splnena podmienka 3 z definicie mnohouholnika, mohol by vzniknut napr. taky utvar, aky je znazorneny na obr. 58. Tento utvar volame niekedy mnohouholnikom, ale aby sme ho odli-sili od prave zayedeneho yypukleho mnohouholnika, hoyorime mu neyypukly mnohouholnik.

3. Podia definicie możno w-uholnik zlożit z w-trojuholnikov, które sa neprekryyaju (obr. 58). Sucet ynutornych uhloy yśetkych tychto trojuholnikoy je

n.2R.

Ak odcitame od n.2R sucet uhlov pri yrchole O v tychto trojuholnikoch (4i? = 360°), yyjadrujo rozdieł

n.2R — 4 R

cize

2R (n — 2)

vel’kost suctu yśetkych ynutornych uhlov w-uhol-nika.

4. Spolocny yrchol O yśetkych trojuholnikoy, z których sa składa mnohouholnik, je podia definicie vo ynutri tohto mnohouholnika. n-uholnik je urceny, ak je dane n jeho vrcholov; bodom O może byt

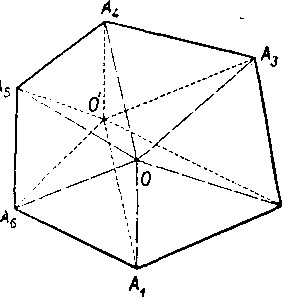
który koIvek z bolov vo vnutri w-uhol-nika. Preto pri oznacovani n-uholnika bod O neuvadzame, ale uvadzamc ibajeho yrcholy (napr. A_xA_tAgA^A_hAg na obr. 59). Toto vśak nie je jediny możny spósob zapisu.

Ine zapisy su napr. AgA^AgAgA^,, alebo A^AgAgA^Ag a pod.

Priklad 1. Dokażte, że priamka leżiaca v rovine yypukleho mnohouholnika, która neobsahujenijaku jeho stranu, ma s obvodom mnohouholnika najyiac dva spolocne body.

Rieśenie (obr. 60). Dókaz uro-    Obr- 59

bime nepriamo. Predpokladajme, że

na priamke p leżia aspoń tri różne body obvodu trojuholnika. Tieto tri body oznacme H, K, L a oznacenie zyolme tak, aby bod K leżał medzi bodmi H, L. Bod K patri urcitej strane QR daneho mnohouholnika. Priamka QR je róznobeżna s priamkou p, lebo podia predpo-kladu priamka p neobsahuje stranu QR. Z toho vśak yyplyya, że body

207

1

Slovo vypukly budeme obycajne vynechavat. Ak budeme hoyorit’ o mnoho¹ uholniku, budeme tym mysliet vypukly mnohouholnik.