1954 Geometria 204

Tieto uhly sa urćuju velmi 1’ahko. Napr. z pravouhleho trojuholnika ACC' ihned’ vyplyva

^sin^ = yW+W+^’

kde cc_x je uhol CAC'.

Obdobne najdeme

b    a

²    ]/a² + b² -f- c^a 3 j/a² -f 6² + c²

kde «₂ = < B'AC', <x_s = <£Z>'AC".

Cvicenie

1.    Urcte vśetky roviny sumernosti dvoch róznobeżnych rovin o, er a od-chylky tychto rovin sumernosti od danych rovin q, a.

2.    Vysvetlite stereometricky princip merania skłonu roviny latou a li-belou podia obr. 52 a svahomerom na obr. 53. Yysvetlite postup v obidvoch pripadoch.

3.    Rozhodnite, które usudky su spravne, które nie, a odóvodnite svoje tvrdenie.

(p, q, r su priamky,    q, a roviny.)

a) Ak je p || q,    je    pr    =    qr.    b) Ak    je    pr    =    <£ qr,    je p    ||    q.

c) Ak je p |[ q,    je    <£    pq    =    <£ qq.    d) Ak    je    <£’ pq    =    <£qq,    je p    ||    q.

e) Ak je 5 || a,    je    pq    =    pa.    f) Ak    je    <£ pq    =    <£ pa,    je q    ||    a.

g) Ak je pq = 0, je <£ rp — rq a obratene.

4.    Ak su 7i a r dve roviny, potom ł’ubovol’na priamka v n urcuje so svojim pravOuhlym priemetom na r (pokial tento priemet je priamka) uhol, który nie je vacśi neż <£ nr. Dokażte to.

5.    Nech su cc, /?, y tri roviny, vsetky rovnobeżne s danym smerom.

Najdite vztahy, które platia medzi uhlami_ ocfi, <źay, y. Urobte diskusiu.    U

6.    V kvadri ABGDA'B'C'D' o rozmeroch AB = a, AD = b, AA' = c urcte tangenty odchylok telesovej uhlopriecky B'D od ostatnych telesovych uhlopriećok.

7.    Vypocitajte dlżku pravouhleho priemetu usecky AB na rovinu q, ak je cc odchyłka priamky AB od roviny q.

8.    Nech p, q su dve mimobeżky a nech <iypq = oc. Dvoma różnymi bodmi A, B na priamke p su vedene royiny a, r kolme na q. Oznacte A_x = q. a, B_x = qr a yypocitajte dlżku usecky A_XB_X.

III. MNOHOUHOLNfKY A TEIESA

1. Vypukle mnohouholmky. Prayidelne mnohouholniky

Trojuholniky a śtvoruholniky (napr. stvoręc, rovnobeżnik a pod.), którymi sme sa zaoberali v planimetrii, su najjednoduchsimi pri-padmi mnohouholnikoy.

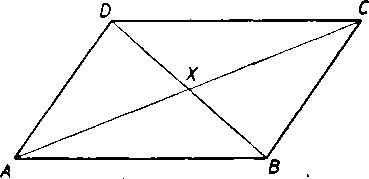
Obr. 55

Vieme, że rovnobeżnik ABGD (obr. 55) możno rozdelif uhlopriec-kami AC, BD na styri trojuholniky f\AXB, /\BXG, AGXD, ADXA, z których każde dva maju spoloćny bod X, pripadne este jednu zo stran XA, XB,

XC, XD; inak uż nemaju dalsi spoloćny bod.

O trojuholnikoch, które maju tu ylastnost, że nijaky z nich neobsahuje body le-żiace vo vnutri druheho, ho-vorime, że sa neprekryvaju.

Trojuholniky, z których sa składa rovnobeżnik ABGD (obr. 55), sa teda neprekryyaju. Podobne sa neprekryvaju ani trojuholniky na obr. 56a; trojuholniky na obr. 56b a 56c sa vśak pre-kryyaju (pozri vyśrafovanu spolocnu casf).

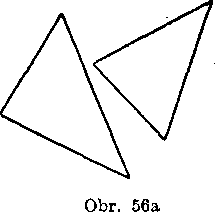
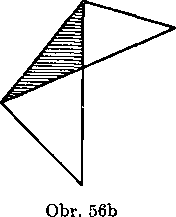
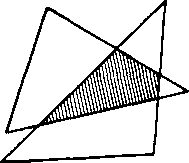
Rovnobeżnik sme teda vytvorili zlożenim urcitych śtyroch nepre-kryvajucich sa trojuholnikov. Obdobnym sposobom móżeme vytvorif

205