1954 Geometria 062

Ve ta 4. Ak platia pre strany a uhly trojuholmkoy A BC, A 'B 'C vz£ahy

•A. A' = A,

je A ABC

A'B' A'C' AB ~ AC A A'B'C'.

Strucnejsie, no menej urćite vysIovojeme vetu 4 takto: Ak maju dva trojuholniky ten isty pomer dvoch stran a ak uh I3⁷, które su nimi zoyrene, su zhodne, potom su podobne.

Dókaz je obdobny dókazu vety ?. (obr. 75). K dvom danym troj-uholnikom ABC, A'B'C zostrojime eśte pomocny trojuholnik A"B"C" tak, aby platilo

A"B" = A'B\ A A” = A A, $ B" = A B.

Podl’a vety uu je potom A ABC ~ A A"B"C". Pomer tejto podobnosti A"B"

je cislo k = —Je teda AU

A"C"    _ A”B" A'B' A'C

AC ~~    ~ AB ~ AB ~~ AC '

Z toho vyplyva A"C = A'C'. Trojuholniky A'B'C, A"B"C"sa zhoduju vo dvoch stranach (A'B' = A"B", A'C' — A"C”) a v zovretom uhle

Poznamka. nazyva£ yetou trojuholnikoy.

(A:A" — <£ A = A: A'); preto je podia vety sus A A'B'C" " ' A A"B"C”. Preto że je A ABC ~ ~ A A"B"C", dostavame podTa vety 1 yztali A ABC~ l\A'B'C, który sme mali dokazaf.

Vetu 4 budeme su o podobnosti

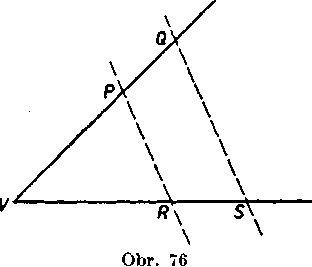
Priklad 10 (obr. 76). Na jedno rameno duteho uhla nanesieme usećky yelkosti a, b, krajne body oznacime P, Q. Na druhe rameno toho isteho uhla nanesieme usecky yelkosti c, d, krajne bcdy ozna

~ je PR\\QS.

cime R, S. Mamę dokazat: ak plati

Riesenic. Oznacme V yrchol dutćho uhla. Pre strany a uhly troj-uholnikoY VPR, VQS platia rztahy

VF VR VQ " VS ’

A PYR = <ŹQVS.

a c

Prvy z oboch vzt'ahov móźeme prepisat na vzt’ah — = ktoreho

platnost sme predpokladali. Podia vety su je A VQ8 ~ A YPR, a teda A VPR = A VQS. Z toho podia znamej vety vyplyva, że PR\\Q8.

Dokazana veta je obratenou vetou z prłkladu 6 cl. 2.

Vety 2 a 4 su vety o podobnosti Iubovol'nych trojuhołnikov. Możno odvodit eśte jednu vetu o podobnosti trojuholnikoy, która je obdobou vety S,m o zhodnosti trojuholnikov. Na ukażku si ju odvodime pre pravouhle trojuholniky.

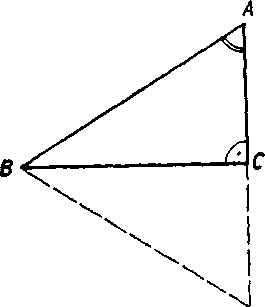
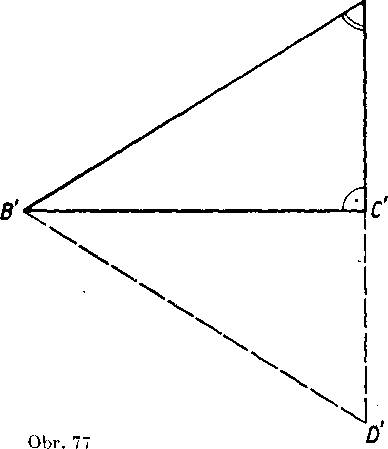
Veta 5. Ak pre strany prayouhleho trojuholnika plati yzfah

A'B' A'C'

AB ~ AG ’

priCom uhly A C = AC' su praye, je A ABC ~ A A'B'C'.

63