1954 Geometria 212

Okrem toho krużnica k opisana K-uholnlku M' prejde opisanym premiestenlm do krużnice, która je sustredna s krużnicou k opisanou n -uholnlku M.

Hladana rovnolahlost ma teda stred v bodę O a koeficient

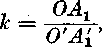
alebo (co je to iste)

Cvj cenie

/j^^tJhlopriccka yypukleho w-uholnlka je usećka, której krajne body su dva nesusedne vrcholy. Dokażte, że w-uholnlk (n ^ 3) ma

— n(n — 3) uhlopriećok.

Z

fł. Dokażte, że uhlopriecky yychadzajuce z jedneho vrcholu yypukleho 7i-uholnlka (n > 3) rozdeluju tento w-uholnlk na n — 2 troj-uholnikoy.

Obr. 66

Z. Który w-uholnlk ma tolko uhlopriećok ako stran?

4- Poużitlm yysledku cvicenia 2 znovu dokażte, że sucet ynlitomych uhlov yypukleho n-uholnlka je 2R (n—2).

Dokażte, że spojnice bodu, który leżi vo vnutri strany A_XA₂ yypukleho n-uholnlka, s jeho zyyśnymi yrcholmi rozdeluju tento w-uholnlk na w — 1 trojuholnlkoy.

6. Dokażte, że dve usećky AB, CD, które sa pretinaju v bodę O leżiacom vo vnutri każdej z nich, urćuju vypukly stvoruholnik ABCD.

A Je dany sedemuholmk ABCDEFG, usećka A'B' = AB a bod M, który neleżi na priamke A'B' (obr. 67). Zostrojte sedemuholmk A' B' C' D' E' F' G', który budę zhodny s danym sedemuholnikom a budę leżat v polrovine A'B'M.

8. Dokażte, że każdy w-uholnik, ktoreho vśetky strany a vnutorne uhly su zhodne, je pravidelny.

^ Dokażte, że każdy pravidelny n-uholnik ma prave n osi sumernosti.

D    C

Obr. 67

9> Ak zostrojime vśetky uhlopriecky pravidelneho patuhelnika, ob-medzia tieto uhlopriecky pafuholnik. Dokażte, że Yzniknuty paf-uholnik je pravidelny.

11. Ak je a_n vel’kost strany pravidelneho w-uholnika vpisaneho do krużnice o polomere r, a_2n vel’kost strany pravidelneho 2n-uholni-ka, który je vpisany do tej istej krużnice, plati rekurentny vztah

Dokażte to.

213