1954 Geometria 272

2. Ked’ postupne zdvojnasobujeme pocet stran pravidelneho n-uhol-nika opisaneho krużnici k o polomere r, obsahy vzniknutych mno-houholnikov tvoria klesajucu postupnost, ktoru oznacime

Qn> $2n> Qin> Qsm Ql$n’ • • •> QnJ^c> • • •

Pritom podia vzorca (4) na str. 267

_n 2+ 2 B

Qn = »»-^atg —•

* 3. Postupnost obsahov vpisanych mnohouholnikov je zhora ohra-nicena.

4.    Postupnost obsahov opisanych mnohouholnikov je zdoła ohra-nicena.

5.    Obidve postupnosti maju teda podia vety o ohranieenej rastucej (klesajucej) postupnosti limit. Ukażeme, źe limity obidvoch postupnosti sa navzajom rovnaju a źe sa rovnaju obsahu kruhu o polomere r.

Poznamka. Prv neź prikrocime k dókazom pomocnych tvrdeni

2R

1 — 6, musime si uvedomit, że n 3, także uhol — je ostry. Preto

,    • 2i?

1 > sm — > 0, n

2 R

1 > cos — > 0, n

tg

^>0.

n

1. Ked zdvojnasobime pocet stran pravidelneho n-uholnika vpisa-neho do krużnice, zvacśi sa jeho obsah, t. j. plati

^Pn < ^P2n>

kde P_n je obsah n-uholnika, P_in obsah 2n-uholnika (obr. 29, kde sme pre urćitost zvolili n = 6).

Skutocne, każdy vpisany 2n-uholnik możno zlożit z vpisaneho n-uholnika a 2n zhodnych rovnoramennych trojuholnikov (na obr. 29 su vyśrafovane).

Ak oznacime który kol vek z vyśrafovanych trojuholnikov P, potom podia podmienky 2 tej to definicie plati

^P2n = ^Pn + ^nP-

Pretoże podia podmienky 1 definicie obsahu

nP > 0,

plati

P-tn > Pn-

Tym sme dokazali, źe postupnost obsahov

p p p p p    p k

je rastuca.

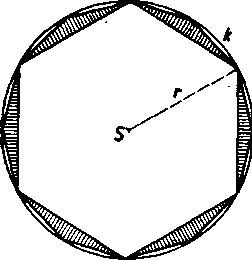
Obr. 29

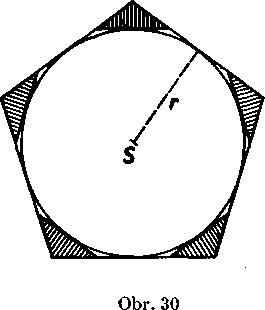
2. Ak zdvojnasobime pocet stran pravidelneho n-uholnika, który je opisany krużnici, zmensi sa jeho obsah, t. j. plati

Qn ^ Q‘2n-

kde Q_n je obsah n-uholnika, Q_2n je obsah 2n-uholnika (obr. 30, kde n = 5).

Skutocne, każdy opisany n-uholnik możno zlożit z opisaneho 2n-uholnikaa2nzhodnychrovnoramennychtrojuholnikov (na obr. 30 su vysrafovane). Ak oznacime obsah ktorehokol’vek z vysrafovanych trojuholnikov Q_n. potom podia poznamky 2 k definicii obsahu mnoho-uholnika a podia podmienky 2 tej to definicie plati

Qn = Q‘ln + nQ.

Pretoże podia podmienky 1 definicie obsahu

nQ > 0,

plati

Qn Q‘in-

273