1954 Geometria 230

Obidva kruhy, v których roviny «, /S pretinaju valcovy priestor, nazveme podstavami valca.

Mnożina stran valca yyplńa piast valca. Piast a obidve podstavy tvoria povrch valea. Vzdialenost rovin oboch podstay je ryska valca.

Valec, który yznikne z rotacneho yalcoyeho priestoru, vola sa rotacny valec. Pri rotacnom valci yyska sa royna vel’kosti strany.

Definicia. Dana je kruznica k v rovine p a bod V, który leżi mimo q (obr. 86). Mnoźina priamok, które prechadzaju bodom V a pretinaju o

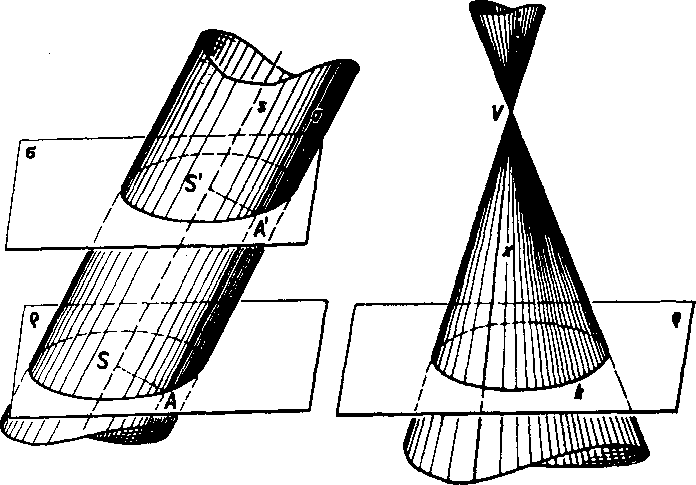
Obr. 85    Obr. 86

v bodoch kruhu k, yyplńuje kużelbyy priestor. Priamky kużel’oveho priestoru, które pretinaju krużnicu Ic, yyplńaju kużeloyu plochu.

Krużnicu z predoślej definicie budeme volat riadiacou kruźnicou kużeIoveho priestoru alebo kużel’ovej płochy. Bod V je yrcholom priestoru alebo płochy. Ak je priamka, która spaja yrchol so stredom riadiacej krużnice, kolma na rovinu krużnice, vola sa kużeloyy priestor (płocha) rotacnym.

Priamky kużelbyeho priestoru, które nie su priamkami kużel’ovej płochy, su priamky ynutorne a ich body yyplńaju ynutro kużeloyeho

priestoru; vrchol V vsak nepoćitame do vnutra kuźel'ovelio priestoru.

Każda priamka kużel’oveho priestoru je yrcholom rozdelena na dve polpriamky. Polpriamky, które maju społocny bod yyplńaju s kru-hom k (krużnicou k) cast kużel’oveho priestoru (płochy), ktoru yoiame prilahlou k riadiacej kruźnici.

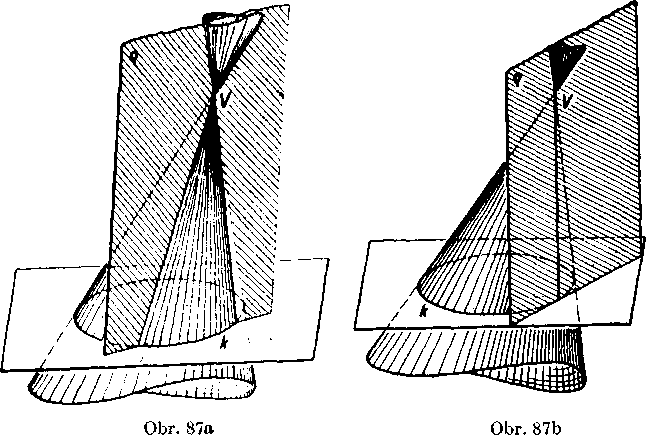
Aj pri kużeloyom priestore zaradzanie pójmy vrcholova priamka a vrcholova rovina, których definicie vyslovite sami. Vrchołova rovina pretina kużel’ovu plochu bud’ vo dvoch A^rcholoyych priamkach (secna royina), bud v jednej vrcholovej priamke (dotykora rovina), bud’ len vo vrchole V (rovina nesecna) (obr. 87 abc).

Teraz uvedieme definiciu telesa, które sa rola kruhoyy kużel.

Definicia: Kruhoyy kużel’ je utvar, który je społocny casti kuże-l’oveho priestoru prilahlej k riadiacej kruźnici a polpriestoru gV, kde q je rovina riadiacej krużnice a V vrchol kużelWeho priestoru.

Riadiaci kruh je podstaya kużel’a a prisluśna krużniea kruhoAa hrana. Yrchol V je yrcholom kużela. łJseeky na priamkach kużeł’ovej płochy ohranicene rrcholom a priesecikom priamky s rovinou pod-stavy volaju sa strany kużela. Mnożina stran yyplńa piast kużela. Podstava a piast tvoria povrch kużela. Body kużela,, które nepatria povrchu, su vnutorne a yyplńaju vnutro kużela. Vzdialenost yrcholu od royiny podstayy je yyska kużela.

231