1954 Geometria 238

rovina rovinou hlavnou, volame obidva odseky polgułami. Kruh v sec-nej rovine, który urcuje odsek, je podstavou odseku, prisluchajuca kruźnica je kruhova hrana. Utvar. który je spolocny odseku a gul'ovej płoche, vola sa gul’ovy yrchlik. Gul’ovy vrchlik a podstava tvoria

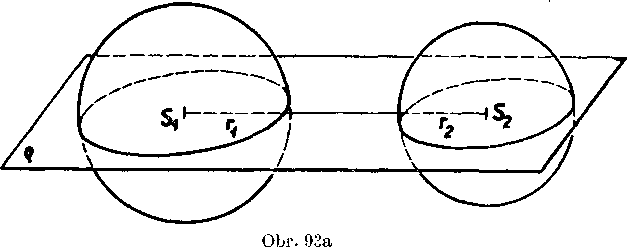
povrch odseku. Kolmica Ycde.ua stredom podstavy odseku na jej rovinu pretina vrchlik v bodę U. Yzdialenost bodu U od roviny pod-stavy vola sa vvska odseku alebo yyśka yrchlika.

jSTech su dane dve różne rovnobeżne secne roviny q aa gul’ovej płochy. Tjtvar, który je spolocny guli a vrstve qo je gul’ova vrstva. Obidva

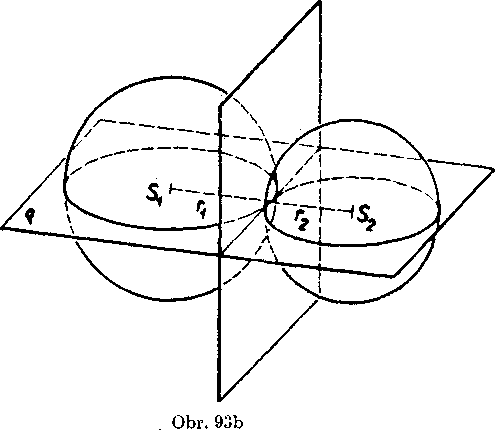
kruhy v rovinach q a a su podstawy; prisluchajuce krużnice yolaju sa kruhove hrany. Utvar, który je spolocny gul’ovej vrstve a guloyej płoche, je gul’o\y pas. Gul’ovy pas a obidve podstavy tvoria povrch guloyej vrstvy. Vzdialenost obidvoch podstay je vyśka gu!ovej vrstvy alebo guloyeho pasa.

Prlklad 7. Urobte diskusiu yzajomnej polohy dvoch gul’ovych

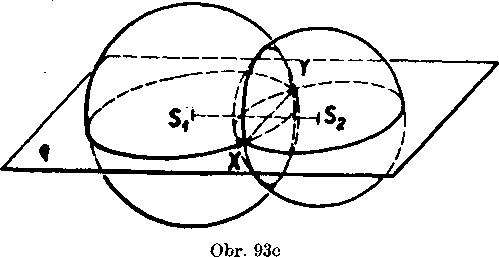
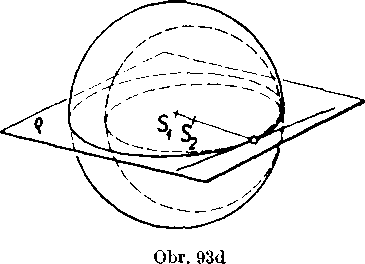
Riesenie (obr. 93abcde). Oznacme 8_V S₂ stredy a r_v r₂ polomery obidvoch gul’ovych plóch. Ńajskór preskumame pripad, ked’ S_x s S₂ ; v tomto pripade yolame obidve gul’ove płochy sustredne. Ak je v tomto prlpade i\ =£ r₂, nemaju gul’ove płochy spoloćne body, ak je r₁=

= r₂, su totożne a maju vśetky body spoloćne. Tieto zavery vyplyvaju ihned’ z definłcie.

Całej budeme teda predpo kladat, że S₁ ^ S₂. Priamkou SiS₂ povedieme Iubovol’nu ro-vinu q, która pretne obidve gu-Iove płochy v hlavnych krużni-ciach. Z planimetrie teraz vieme, że obidve hlavne krużnice y o bud’

(1)    nemaju nijaky spolocny bod, ak plati S_XS₂ > r₁Ą-r₂ alebo S_l8₂ < < | r₁ — r₂ j (tento druhy pripad nemóże nastaf, ak je r_x = r₂), bud’

(2)    obidve krużnice maju na priamke S_XS₂ jediny spolocny bod, ak je S_XS₂ — r_x + r₂, alebo S_XS₂ = j r_x — r₂ j (ani tento druhy pripad nie je możny, ked’ r_x = r₂), bud’ napokon

239