1954 Geometria 220

Cvićenie

ke spolocne utvary maju

a)    vrcholova rovina a hranolovy priestor;

b)    nevrcholova priamka a hranolovy priestor (hranolova płocha);

c)    vrcholova priamka a hranol (povrch hranola);

d)    ncvrcholova priamka a hranol (poYrch hranola);

e)    vrcliolova rovina a hranol (povrch hranola);

f)    nevrcholova rovina a hranol (povrch hranola) ?

2. Urcte vsetky roviny sńmernosti hranoloveho priestoru, ktoreho riadiacim mnohouholnikom je śtvorec a leżi v rovine kolmej na smer hran.

3. Dokażte: priesek nevrcholovej roviny s hranolovym priestorom je rovnobeżnik, ak je riadiacim mnohouholnikom rovnobeżnik. Możno tuto vetu obratitd

4. Vyslovte definiciu kvadra a kocky.

, 5. Je dana kocka v zakladnej polohe ABCDA'B'C'D', 8 je stred steny ABCD, M stred branydD, Q stred hrany A'B'. Riadiacim stvoruholnikom hranolovej płochy je śtvoruholnik AB8M, smer priamok je dany priamkou p || AA'. Narysuj te priesek hranolovej płochy a) s priamkou QG, b) s roYinou QBG.

6.    Je dana kocka ABCDA'B'C'D' v zakladnej polohe, P je stred hrany C'D', Q stred hrany AB. Riadiacim trojuholnikom hranolo-vej płochy je trojuholnik ABD, smer priamok je dany priamkou p\\AP.

a)    Narysuj te spolocny utvar priamky D'Q a płochy.

b)    Urcte konśtrukcne a Yypoctom odchylku priamok hranolovej płochy od roviny ABD; to iste urobte pre odchylku priamky D’Q a smeru p.

c)    Urcte konśtrukcne a vypoctom skutocnu vel'kosf usecky, kto-ru oddeluje hranolova płocha na priamke D'Q.

7.    V kocke ABCD A 'B'G'D' su K, L, M, N stredmi hran AB, BC, CD, DA; dalej P a P' su po poriadku bodmina AB a A'B', a to takymi,

że BP = A'P' — ~ AB. Hranolova płocha H₁ ma riadiaci stvorec

KLMN a smer priamok je dany priamkou p [j AA', hranoloYa płocha H_a ma riadiaci trojuholnik PP'A a smer priamok je dany priamkou q j| AD. Narysujte lomene ciary, v których hranolova płocha H₂ pretina hranoloYu plochu Hj^.

® Rozmery kvadra su x, 2x, 3x. Urcte vel’kosfi telesovej uhlopriecky a odchylky uhlopriecky a hran.

9. Na j di te vsetky roviny sumernosti kvadra a kocky.

10.    Opakujte predośle cYicenie pre pravidelny n-boky hranol.

11.    Urcte pocet telesovych uhlopriecok w-bokeho hranola a dokażte, że każdy vnutorny bod telesovej uhlopriecky leżi yo Ynutri hranola.

/l2) Pravidelny śestboky hranol ma dva druhy telesovych uhlopriecok. Urcte ich velkosti, ak su a, v po poriadku Yelkosti hrany podstavy a vyśky telesa.

13. Dokażte, że IubovoIny hranol ma o dve hrany menej, neż cini sucet vsetkych stien a vrcholov (Eulerov vztah).

14.    Dokażte:

a)    PoYrch rovnobeżnostena sa składa zo siestich rovnobeżnikov, z których dva a dva naprotivne su zhodne. Rovnobeżnosten możno povażovat trojakym sposobom za hranol; vysYetlite.

b)    Każde dve telesove uhlopriecky sa naYzajom rozpoluju. Vśetky prechadzaju jednym bodom, nazyvanym stred rovnobeżno-stena.

15.    Dokażte, że existuje rovnobeżnosten, zvany klenec, który je ob-medzeny śiestimi naYzajom zhodnymi kosośtvorcami.

3. lhlanoyy priestor, ihlanova płocha, ihlan

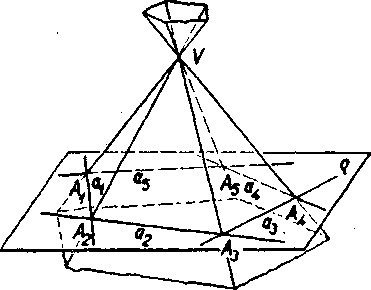
Obr. 73

Definicia (obr; 78). Je dany vypukly mnohouholnik A₁A_t.. ,A_n, który leżi v rovine o, a dalej bod V, który neleżi v rovine q. Mnożina priamok, które prechadzaju bodom V a pretinaju rovinu q v bodoch mnohouholnika, vyplńa ihlanovy priestor. *

Mnohouholnik A_xA_t.. .A_n z predoślej deiinicie bude-me volaf riadiacim mnohouholnikom ihlanoveho prie-storu, bod V vrcholom ihlanoveho priestoru.

Tie priamky ihlanoveho priestoru, które pretinaju obvod riadiaceho mnohouholnika, YypIhajutzY. ihla-novuplochu. Ostatnepriam-

221