1954 Geometria 086

Cviceńie

1.    VeIkost uhla v stupnoch je 45°; 80°30'j 6°50'; 29,2°.

Vyjadrite v dielcoch.

2.    Yelkosć uhla v dielcoch je 235; 1100; 862; 1 500.

Yyjadrite ju v stupnoch a v minutach.

3.    Aka je v dielcoch veIkost zorneho uhla telegrafnej tyce (6 m vyso-kej), która stoji vo vzdialenosti 1 km, 387 m, 120 m, 25 m od pozo-rovateIa? Zorny uhol v poslednom pripade vypocitajte jednak po-użitim funkcie tangens, jednak podia dieIcoveho pravidla a ohidva vysłedky porovnajte.

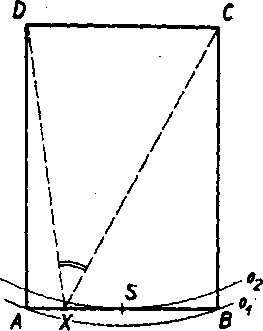
Obr. 100

4. Obr. 100. ABCD je obdlżnik, v ktorom je AB < BC. Ak prebieha bod X useckou AB, meni sa zorny uhol <C OXD, Naj mensie su zorne uhly <£ GAD = <£ Ć7B.D, najvacśi je zorny uhol <f,. CSD, kde A je stred usecky AB. Dokażte to. Navod: Zostrojte obluky o_v o.,; z ich bodov vidiet usecku CD pod uhlom CAD alebo

< CŃD.

5.    Obr. lOl.JLBOPje obdfżnik,ktoreho rozmery su vpomere AB: BC = = 1:5. Ak prebieha bod X useckou AB, je ve!kost zorneho uhla

CXD, zaokruhlena na cele diełce, pre vsetky body X rovnaka. Dokażte to s poużitim vysledku cvicenia 4.

6.    Budovu, 20 m vysoku, vidime pod vyśkovym zornym uhlom 6 diel-cov. Aka je dlżka priecelia budovy, które vidlme z toho isteho stanovisfa pod zornym uhlom 14 dielcov?

7.    Pozdlż cesty ide telegrafne vedenie. Na stanovisti 8 boli zmerane

zorne uhly tyci, stojacich v bodoch A, B, G, 1), E, F\ ich vel’kost v dielcoch je 10, 14, 15, 9, 8, 6. Okrem toho boli v dielcoch zmerane horizontalne uhly:    ASB = 40, B8G = 30, ^ CSD = 45,

DSE — 50, -if.. ESF — 35. Nacrtnite vo vhodnej mierke priebeh useku cesty medzi bodmi A, F.

8.    Podia vzoru z cvićenia 8 najdite obdobnu situaciu v terene, urób te potrebne meranie a nakreslite nacrtok.

9.    Ylak ide po priamej trati, która je v priecelnej polohe. Telegrafnu tyc, która je od pozorovatel’a 700 m vzdialena, minie za 8 sekund. Zorny uhol vlaku je 170 dielcov. Aka je dlżka vlaku a akou rych-lostou sa pohybuje ?

5. Funkcie sinus, kosinus a kotangens

V clanku 2 (str. 72) definovali sme funkciu tangens pomocou pome-ru dvoch odvesien. To bolo możne preto, że pomer odvesny proti-lahlej k uhlu x ku odvesne prilahlej k uhlu « je zavisly len od uhla a nie od pravouhleho trojuholnika, z ktoreho vychadzanie. Obdobnu vlastnosf ma pomer ktorychkol’vek dvoch stran pravouhleho trojuholnika; preto móżeme zaviest pomocou pomerov stran celkom sest funkcii. Tieto funkcie sa volaju goniometricke; jedna z nich je funkcia tangens. Teraz uvedieme este dalśie tri, które sa v matematike casto poużivaju.

1.    Pomer protirahlej odvesny k uhlu a ku prepone je sinus alfa, skratka sin «.

2.    Pomer prilahlej odvesny k uhlu <x ku prepone je kosinus alfa, skratka cos oc.

3.    Pomer prilahlej odvesny k uhlu ot k protilahlej odvesne uhla a je kotangens ot, skratka cotg ot.

87