1954 Geometria 314

Cvicenie

Urcte objem prayidelneho śtvorstena o hrane a.

Urcte objem prayidelneho w-bokeho ihlana o podstavnej hrane * a a bocnej hrane b.

Specialne jfi n = 4, b = 2a; W) n = 6, b — 2a.

3.    Dokażte: Objemy podobnych ihlanov su v roynakom pomere ako tretie moeniny hran, które si v podobnosti zodpovedaju.

4.    V akom pomere su objemy dyoch pravidelnych śtvorstenov, z których jeden ma yrcholy v tażisku stien druheho?

/o. Aka velka je podstavna hrana pravidelneho trojbokeho ihlana o yyśke v a objeme V ?

6.    Urcte objem styorbokeho ihlana s podstavou pravouhleho rovno-beżnika. Bocne hrany tohto styorbokeho ihlana su rovnake, ak je dana yyśka v ihlana a uhly cc, fi, które urcuju dve susedne bocne steny s podstavou.

Oiselne: a) v = 30 cm, « = 60°, /5 = 45°;

v = 10 cm, « = 63°, 0 = 72°.

7.    Urcte objem prayidelneho w-bokeho ihlana o bocnej hrane 6, która ma od podstayy odchylku fi.

Ćiselne: a) n = 10, 6 = 7 dm, = 72°; b) n — 5, 6 = 25 cm, (3 = 60°.

&. Urcte objem prayidelneho w-bokeho ihlana o yyśke v, ktoreho bocna stena ma od podstayy odchylku oc. Oiselne:

4 « = 4, v == 1,5 dm, <x = 60°; b) n = 8, v = 37,5 cm, cc = 65°.

9. Dokażte: Ak je V objem zrezaneho ihlana, v jeho yyśka , p_v obsahy jeho podstay, potom neyyhnutne plati

2F< (p_t + p₂)v< 3F.

10. Vyśka prayidelneho śtyorbokeho zrezaneho ihlana je v, sucet obsahoy oboch zakladni p, objem V. Urcte yelkosf podstavnych hran (predpoklada sa 2V < pv < 3V). ćiselne: v = 3 cm, p = 41 cm², V — 61 cm³.

łl. Pravidelny śtvorboky zrezany ihlan ma podstavne hrany a_v a₂ (kde a_x > a_% > 0) a vyśku v. Urcte objem ihlana, który dopina dany ihlan na uplny prayidelny śtyorboky ihlan.

Ćiselne: a_x = 4, a₂ = 1, v = 2.

12. Ako treba volit rovinu q, która prechadza jednou hranou prayidelneho śtyorstena, aby yzniknute telesa mali objemy v danom pomere p : q {p, q su kladne ćisla) ?

4S. Urcte objem prayidelneho zrezaneho n-bokeho ihlana s podstay-nymi hranami % a₂ (kde a_x > a₂).

Bocne hrany tohto ihlana maju od podstay odchylku tx.

14. Podstayy styorbokeho zrezaneho ihlana su dya obdlźniky; spoj-nica stredoy oboch obdlżnikov je kolma na podstayy. Rozmery jedneho obdlżnika su a_v b_x, obvod druheho je o₂ [(°2) ^    + 6i)].

Vzdialenost podstay je d. Urcte objem telesa. Ćiselne: a_x = 54, b_xr= 30, o_a= 112, d = 12.

45. Zrezany pravidelny ihlan s podstavnymi hranami a_v a₂ je rozde-leny royinou rovnobeźnou s rovinami podstay, która rozpoluje jeho vysku, na dva zrezane ihlany; aky je pomer objemov tychto ihlanoy ?

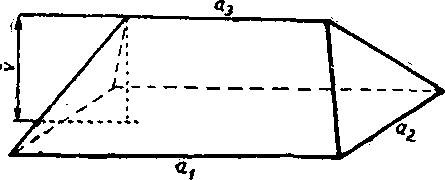
Obr. 68

16.    Zrezany ihlan je rozdeleny rovinou rovnobeżnou s podstavami p_± a p₂ na dva zrezane ihlany, których objemy su v pomere m : n (m,n su kladne cisla); v akom pomere su ich vyśky ?

17.    Z trojbokeho hranoloveho priestoru yytinaju dve rozlićne roviny (które nie su vrcholove a su bud’ roynobeżnć, bud’ maju priesecnicu mimo hranoloveho priestoru) patsten (jeden pripad je zobrazeny na obr. 68). Urcte jeho objem, ak poznate 1. vel’kosti a_v a₂, a₃ jeho hran, które leżia na hranach hranolovej płochy, 2. yzdialenost 6 hran a_v a₃, yzdialenost v hrany a₃ od royiny hran a₂, a₃.

315