1954 Geometria 114

Cvicenie

1.    Narysujte pravidelny sestuhołnik o strane 3,5 cm, zvol'te vo vnutri bod M a zostrojte k nemu utvar rovnol’ah]y podia stredu M. Koe-

3

ficient rovno!ahlosti zvol’te--

2.    AB, CD su dve rovnobeżne nezhodne usecky, które neleżia na jednej priamke. Urcte stredy a koeficienty vśetkych rovnol’ahlosti, które prevadzaju usecku AB do usecky CD. Navod: Uvaźte, że bod A prejde bud’ do bodu C, bud' do bodu Z).

3.    Opakuj te cvicenie 2 pre dve nezhodne iisecky, które leżia na jednej priamke.

4.    Dokażte, że rovnoIahlosf prevedie stred iisecky AB do stredu jej obrazu A'B'.

5.    PQRS, P'Q'R'S' su dva nezhodne śtvorce, pre które plati PQ \\P'Q'. Urcte stredy a koeficienty vsetkych rovnol’ahlosti, które preyadzaju §tvorec PQRS do śtvorca P'Q'R'S'. Navod: Uvażte, że bod P może prejsf do ktorehoko!vek z bodov P', Q', R', 8'.

6.    Obr. 131. ABCD je lichobeżnik so zakladnami AB, CD. Dokażte, że priesecik priamok AC, BD, priesećik priamok BC, AD a stredy oboch zakladni leżia na priamke. Navod: Poużite vysledok z cvicę-nia 2.

7.    Poużite vysledok z cvicenia 6 na to, aby ste zostrojili stred danej usecky iba pomocou dvoch trojuholnikovych pravitok.

8.    Dokażte, że rovnol’ahlosf so stredom v tażisku trojuholnika a s koe-ficientom — — prevadza

U

a)    każdy vrchol trojuholnika do stredu protilahlej strany;

b)    priamku, na której leżi vyśka do osi strany;

c)    priesecik vyśok do stredu opisanej krużnice.

Co możno povedat na zaklade vysledku c) o fażisku, o prieseciku vyśok a o strede opisanej krużnice? Presvedcte sa pomocou kon-śtrukcie.

9.    RYS, TVW su dve róznobeżky, TUSV je rovnobeżnik. Co vyplnia stredy rovnol’ahlosti, które prevadzaju uhol <f, VTU a) do uhla

WVS, b) do uhla <£ RVT\

2. Pouźitie rovnol'ahlosti

RovnoIablost sa poużiva pri rieśeni mnohych konstrukcnych uloh. Uvedieme niekolko prikladov.

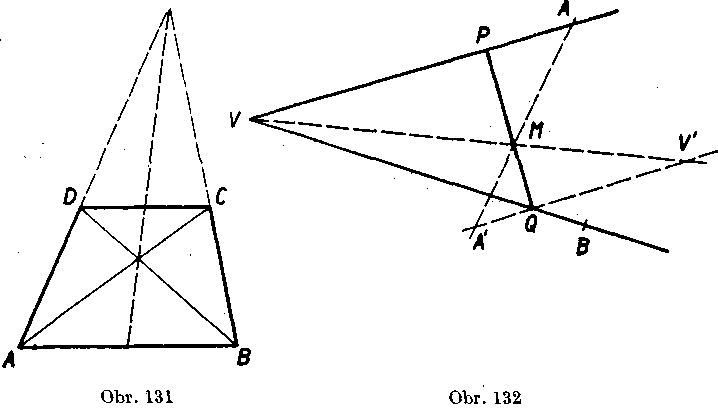
Priklad 5. (Obr. 132). Vo vnutri duteho uhla <C A VB je dany bod 31. Marne zostrojit usecku PQ tak, aby bod P leżał na ramene VA, bod Q na ramene VB a aby platilo

P3I\Q31 = 3:2.

Rieśenie. Predpokladajme, że hladana usecka PQ je uż zostrojena

2

(obr. 132). Potom rovno!ahlost so stredom M a koeficientom — —

O

prevadza bod P do bodu Q. Ta ista rovnoIahlost prevadza priamku VA do priamky V'A', która je rovnobeżna s VA; na priamke V'A' leżi bod Q.

Priamku V'A' vieme zostrojit, lebo F', A' su obrazy bodov VA

2

v rovnol’ahlosti so stredom Mas koeficientom — —. Pretoże je

V'A' || VA a pretoże priamka V'A' leżi vo vnutri polroviny VAM, pretne priamka V'A' polpriamku VB v urcitom bodę Q. Priamka QM pretne polpriamku VA v bodę P, który je v naśej rovnorahlosti vzorom bodu Q.

Z predchadzajuceho vykładu vyplyva, że uloha md pri każdom uhle a pri każdej polohe bodu M jedine rieśenie.

115