1954 Geometria 154

b) V cviceni lb zistite priesećiky predtżenych stran trojuholnika A'B'C' s rovinou ABC. Cvicenie lb opakujte pre pripad, że DA' = 4 a A'B' \\AB.

3. Yo vnutri hran śtvorstena ABCD vol'te body takto: M na AB, N na CD, P na AD, Q na BD, B na CD tak, że DN < DR, 8 na

AD tak, że DP < D8. Urcte spo-D    locny bod rovin ABC. QRS, MNP

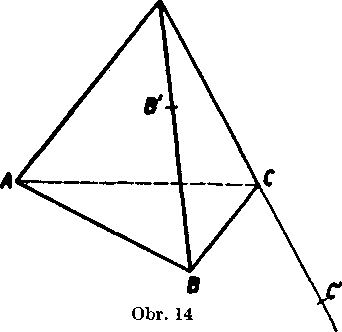
(pokial existuje).

4. Vo vnutri hran C'D', BB' kva-dra ABCDA'B'C'D’ zvo!te body M, N.

a) Zobrazte vo vol'nej projekcii rovnobeżky CM \ | NP, kde P je bod priamky A'B' a zistite priesecnice p, p' roviny q = CMN s rovinami obidyoch podstav kvadra.

D.

b)    Urcte priecku XY mimobeżiek BD, A'C', która leżi v rovine q z cvicenia a).

c)    (Nicienia a), b) rieste konśtrukcnym poużitim siete daneho kvadra a urcte voTkost usecky XY. <Vol’te AB = 5; AD = 3; AA' = 6; CM = 3,5; BN = 3,5.)

f t

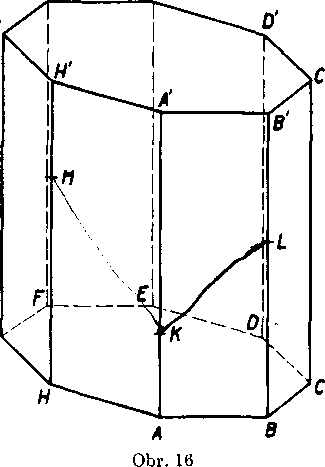
medzi B, B' a bod M medzi H,H'.

5.    Je dany stvorsten ABCD. Na usecke AD urcte bod

M tak, aby AM = ~ AD,

a na usecke BC urcte bod N tak, że BN = 3BC. Zobraz-te taku priecku p mimobeżiek AB, CD, aby bolo p \\MN.

Kolko rieśeni ma tato ulo-ha ? Kędy uloha nema riese-nie? l7lohu rieste konstruk-cne ako v cviceni 4.

6.    Je dany pravidelny osembo-ky hranol (obr. 16),t. j.teleso obmedzene dvoma zhodnymi pravidelnymi osemuholnik-mi ABCDEFGH a A 'B'C' D’E'F'G'H' a ósmimi zhodnymi obdlżnikmi AB B'A' atd’. Zostrojte vypukly mno-houholnik, v ktorom rovina KLM pretina teleso. Bod K zvol’te medzi bodmi A, A', bod

4. Rovnobeżnosf priamok a royin

Skumanie vlast-nosti incidencie nas viedlo k zavedeniu pojmu rovno-beżnosti; teraz si preberieme niektóre vlastnosti rovnobeżnych priamok a rovin.

Z piateho Euklidovho postulatu sme odvodili v planimetrii v 7. rocniku tuto poućku:

Veta 4. K danej priamke możno danym bodom viesl jedinu rovno-beżku.

155