1954 Geometria 128

3.    Zostrojte spolocne dotycnice dvoch krainie, które maju vonkajśi dotyk. Zistite, kędy sń dve krażnice zhodne a kędy su nezhodne.

4.    Dlżkou spolocnej dotycnice dvoch krużnic volame vzdialenost jej bodov dotyku. Oznacme r_v r₂ polomery oboch krużnic, s vzdiale-nosfi ich stredov. Dokażte, że dlżka vonkajśej spolocnej dotycnice je J/s² — (r₁ — r₂)², dlżka vnutornej spolocnej dotycnice je

y«² — (r_x + r₂)².

Pri diskusii preberte vśetky możne vzajomne poloby dvoch krużnic.

5.    Najmenśia vzdialenost dvoch kolies je 2 dm, dlżka vonkajśej dotycnice je 2,4 m, dlżka vnutornej dotycnice je 1 m. Vypocitajte vzdia-lenost hriadel’ov a polomery kolies.

6.    Polomery krużnic su r₁ = 3,4 cm, r₂ = 5,8 cm, vzdialenost ich stre-dov je 11,3 cm. Vypocitajte yelkost ostróho uhla, który zviera so spojnicou stredov a) vonkajśia dotycnica, b) vmitorna dotycnica.

7.    Narysuj te dve krażnice, które maju vnutorny dotyk a zostrojte ich stredy rovno!ahlosti.

8.    Zostrojte trojuholnik S₁S₂S₃ so stranami S_XS_Z = 4 cm, S₂S₃ = 5 cm, S₃S_X = 6 cm. Około bodov 8_V S₂, S₃ opiśte po poriadku krażnice k_v Jc₃, k₃ s polomermi r_x — 1 cm, r₂ = 2 cm, r₃ = 4 cm. Zostrojte v§etky stredy rovnoIahlosti krużnic k_1; k₃; k₂, k₃; k₃, k_v Presvedóte sa, że

a)    vsetky vonkajsie stredy leżia na priamke;

b)    priamka, która prechadza dvoma vnutornymi stredmi, obsahuje jeden vonkajśi stred.

9.    Zostrojte trojuholnik ABC, ak je dany pomer stran AB : AG, uhol <j[4a polomer ypisanej krażnice q.

4. Podobnosf rovinnych utvarov

Teraz sa vratime k otazke z clanku 1, ako definovat podobni utrary. Najskór dokażeme, że pre trojuholniky pląti tato poućka:

Yeta 3. a) Ak su trojuholniky ABO,A'B'C' podobni,możno zostrojif trojuholnikktóry budę zhodny s A A'B’0' (jfiże trojuholnik A'B'C' możno premiestit do polohy A_XB_XC^) tak,że trojuholniky ABC, A-iB-fii budu rovnoIahle.

b) Obrktene: Każde dva trojuholniky, które możno premiestenim uviest do romolahlosti, su podobne.

Dókaz: a) Obr. 148. Ak je A ABG ~ A A'B'G’, je podia vety <£ A = A A'. Na polpriamky opaene k polpriamkam AB, AG nanes-me usećky A'B', A'C'\ takto dostanemebody B_v C_x. Oznacme este A_x = A; podia vety sus je A A₁B₁C₁ ^ A A'B'C'.

A'B'

RovnoI’ahlosC so stredom A as koeficientom--AB P^rev^⁽^^za

vsak bod B do bodu B_x a aj bod C do bodu C_x, lebo AC_X — A'C — A'B'

= —r-g- AG. Tato rovnoIahlost prevadza teda A ABC do l\,A_xB_xO_x, AB

co sme chceli dokazat.

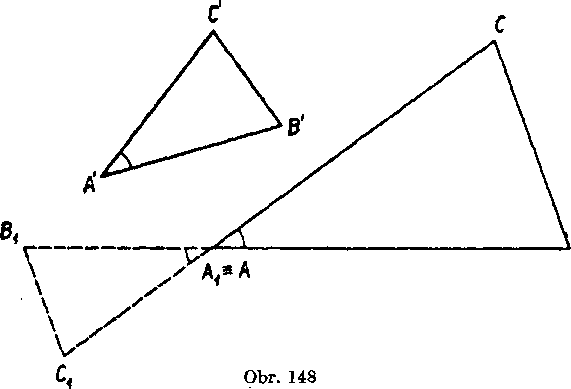
b) Nech su ABC, A'B'G' dane dva trojuholniky, A_XB_XC_X trojuholnik zhodny s A A'B'G' (A A₁B₁C₁ ^ A A'B'C') a sucasne rovnoIahly s A ABG. Podia vety 1 je

A_XB_X ~ k.AB, B_XC_X = k.BG, C_XA_X — k.CA,

kde k je vhodnś kladne ćislo. Kedze A'B' = A_XB_X, B'C' — B_XC_X a C'A' = C_xA_x,)e

A’B' == k.AB, B'C' = lc.BC, C'A' = k.GA, t. j. a A'B'G' ~ a ABC.

Veta 3 nas vedie k tomu, aby sme vyslovili tuto vśeobeonu deflniciu podobnych utvarov: Dva rorinne utvary su podobne vtedy, ked możno

129