1954 Geometria 072

Tento spósob ur cenią stran a uhlov nie je yśak dosf spolahliyy, pretoźe zostrojovanie a meranie uhlov pomocou uhlomeru je nepresne. Niekedy takyto spósob nie je ani możny, ak ide o trojuholniky yelkych

rozmeroy, ako su trojuholniky pri yymeriayani zemskćho povrchu. Tu totiż casto nemożno zmeraf strany tychto trojuholnikoy. Preto mate-matici yynasli pohodlnejsi a pres-nejsi spósob, którym yypoóftame vel-kosti ysetkych. stran a uhloy troj-uholnika z yelkosti danych stran a uh!ov. Tento spósob sa opiera o tzv. goniometricke (uhlomerne) funkcie, s którymi sa teraz ciastocne oboznamime.

B

Obr. 84b

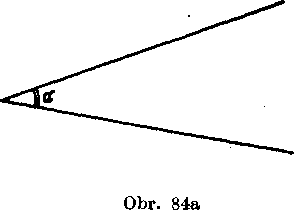
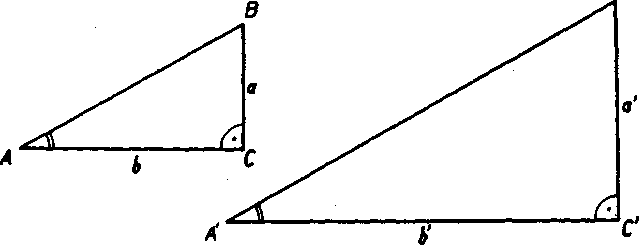
Obr. 84. Nech je dany IubovoIny ostry uhol a. Zostrojme pravo-uhly trojuholnik ABG, który ma uhol cc za ynutorny uhol pri yrchole A. Strany trojuholnika ABG oznaóme obvyklym sposobom o = BG, b = CA, c = AB. Vypocitajme pomer odyesny BG protilahlej k uhlu

cc k odyesne AG prilahlej k uhlu cc, ciże yypocitajme cislo Ak zo-strojźme mimo trojuholnika ABC iny pravouhly trojuholnik A'B'C', ktoreho ynutorny uhol A' budę zhodny s uhlom cc, podia vety uu budę platit, że

A ABC — a A'B'C.

Z toho yyplyya

(1)    a' = hx, b' = Tcb, c' = Tcc, kde k je vhodnó kladne cislo. Zo vz£ahov (1) dostaneme

a/_

V ~ b

To znaci: Pomer protilahlej odvesny ku prilahlej je zavisly od daneho uhla « a nie od pravouhleho trojuholnika, z ktoreho sme tento pomer vypoćitali.

Tym je teda każdemu ostremu uhlu « priradene urcite kladne cislo —• pomer odvesien — które sa vola tangens alfa a które zapisujeme tg «. Skratka ,,tg“ a pismeno tvoria celok, który znaći urcite kladne cislo. Skratka ,,tg“ sama osebe neznaci nijake cislo.

Pri urcovani pomeru odvesien nevychadzame obycajne z ostreho uhla, leź z jeho ve!kosti. Z elanku 1 vieme, źe każde kladne cislo mensie neż 90 móżeme povażovat za vel’kost ostreho uhla v stupńovej miere. Ostrych uhlov tejto yelkosti je nekonecne innoho, ale vsetky su navzajom zhodne a z hocktoreho z nich urcime pomer odvesien. V symbole tga budę pismeno « vźdy znacif yelkosf uhla (cislo).

Obr. 86

Priklad 4. Ureme tg 45°, tg 30°, tg 60°.

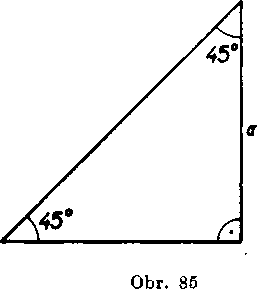
. Riesenie. a) Aby sme uroili tg 45°, zostrojme IubovoIny pravo-uhly trojuholnik, ktoreho jeden uhol je 45°, t. j. zostrojime IubovoIny pravouhly trojuholnik rovnoramenny (obr. 85). Jeho odvesny maju tu istu vel’kos< a\ preto

tg 45°=- = 1.

⁵ a

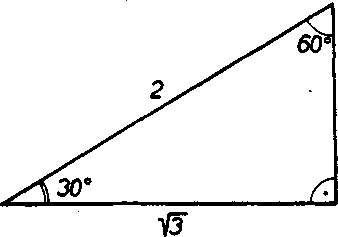
b) Aby sme urcili tg 30° a tg 60°, zostrojme Iubovoiny pravouhly trojuholnik s ostrymi uhlami 30°, 60° (obr. 86). Yieme (pr. 8, str. 58),

73