1954 Geometria 084

v dielcoch a ot vel’kost! toho isteho uhla v stupńoch, je 0 : oc — 1571 : 90, ciźe

(1)    0=17,5*.

Majme teraz zvisly predmet vysky v metrov, który je vo vzdialenosti d km od pozorovatel’a. (Oko pozorovate!a nech je pribliżne vo vyśke dolneho końca predmetu — obr. 98.) Ak oznacime ot vel’kost zornelio uhla v stupńoch, plati podia definicie funkcie tangens

iooo <r

tg oc

/ 1°

Ak nie je zorny uhol vaesl neź 14 móżeme nahradit funkciu tangens priamou umernosfou podia vzorca (3) z ćlanku 1. Je teda

0,0175 ot,

v

1000 d

cize

17,5«=—r. d

Podia rovnice (1) tohto clanku je vsak 0 == 17,5 oc, kde 0 znaci yelkosf zorneho uhla v dielcoch.

Pr eto piat! vzorec

d’

(4)

f?

Obr. 99

co je tzv. dielcove pravidlo; v znad vysku predmetu v m, d jeho vodo-rovnu vzdialenosf od pozorovateTa v km, § zorny ukoi v dielcoch. Diel-cove pravidlo mOżeme pouźif vtedy, ak neprekroci vel'kosf zorneho uhla asi 250 dielcov.

Skutocne z obmedzenia a< 14,5° vyplyva /}< 14,5.17,5 = 250.

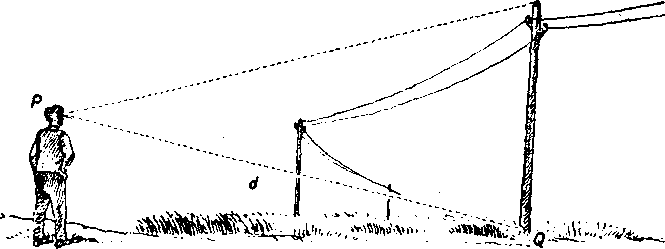
Priklad 13. §es£metrovu telegrafnu tyc vidime pod zornym uhlom 10 dielcov. Ako je daleko?

Rieśenie (obr. 99). Za predpokladu, że trojuholnik PQB je aspon pribliżne pravouhly, móżeme pocitaf podia dielcoveho pravidla alebo pomocou funkcie tangens. Podia dielcoveho pravidla je kde d znaći vodorovnu vzdialenosf tyce. Dostavame teda

d ~ — km = 600 m.

Ak oznacime oc yelkost zorneho uhla v stupńoch, je

tg oc

6

ToOOcT

kde ma d rovnakv yyznam ako horę. Vypocitame

oc —

10

17,5

-4

stupńa, t. j. asi 34'. Z tabulky urclme tg 34' = 0,0099; je teda -kilometra ako podia dielcoveho pravidla. Vypoćet podia dielcoveho pravidla je rychlejśi a menśia presnost pri vaćsine praktickych uloh postaci.

Vo vojenskej praxi poużiva sa namiesto matematickeho dielca tzv. dielec delostrelecky. Pravy uhol ma 1-500 delostreleckych dielcov; delo-strelecky dielec je teda vaćśi neż matematicky dielec a pri poużivani dielcoveho pravidla su potrebne urćite upravy. Tymito upravami sa nebudeme zaoberat.

85