1954 Geometria 092

a z toho

b = a.cotg a.

7t tabulky hodnót kotangens dostaneme cotg «

b — a.cotg a = 11,5

1,2460, a teda

centimetrov.

Yypocitame este uhol /3

90°

51°15'; y = 90°.

Priklad 19. Je zname, źe stań Egyptania poćitali obsah rovnora-menneho trojuholnika tak, że nasobili dlżku polovicnej zakladne dlż-

kou ramena. Aky velky musel byt uhol pri za-kladni, aby chyba pri yypoćte nepresahovala 3% spravneho vysledku?

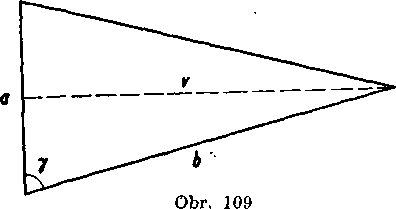
Riesenie. Obr. 109. Oznacme a ve!kos£ za-kladne, b vel’kost rame-na, y yelkosfi uhla pri za-kladni. Vyśka na zaklad-nu rozdęli rovnoramen-ny trojuholnik na dva zhodne pravouhle trojuholniky, których

prepona a jedna odvesna maju ve!kosti b, —. VeIkost vyśky v je teda

v ~ b. sin y a z toho vyplyva spravny vzorec pre obsah:

_ ab

-siny.

Chybny vzorec pre obsah je

ab

P' =

Chyba, której sa dopustame, je

P’ — P = ^-{1—siny).

Podia podmienky ńlohy'musi byt

(1)    P' —P^0,03P,

ciże

ab „    .    , „ „ „„ ab .

— (1 — sin y) ^ 0,03 — sin y.

Po uprave dostaneme

(2)

sin y 5;

1

1,03'

Z obrateneho postupu vyplyva, że ak uhol y spina vzćah (2), spina aj vz£ah (1) a vyhovuje podmienke ulohy. Z tabulky obratenych cisel dostaneme 1 : 1,03 = 0,9709. Hladajme uhol co, pre który

sin co = 0,9709.

Z tabulky hodnót sinusu dostavame co = 76° (zaokruhlene na cele stupne). Pretoże s rastucim uhlom sinus sa zvacśuje, vyplyva zo

vztahu sin y ^    ~ = sin co vz£ah y 3: co.

l.Uo

Chyba pri vypocte nepresahujeteda3% spravneho vysledku, ak je y ^ 76°. Egyptania poużivali skutocne svoju nespravnu formulu len pre trojuholniky s vel’kymi uhlami pri zakladni, które spinali uvedenu podmienku.

Priklad20.(Obr. 110.)Riekamapriamy ą tok, śirku a metrov a rychlosf prudu c_x metroy za minutu. Parnik, który plava na tichej vode rychlostou c₂ metrov za minutu, prevaża z miesta A do miesta B, które je na druhom brehu co najbliżśie k A. Do ktoreho miesta G na druhom (protilahlom) brehu musi parnik namie-rit, aby skutocne pristal v mieste B?

Riesenie. Body A, B, C tvoria trojuholnik s pravym uhlom pri vrchole B.

Ak je t doba prevażania v minutach, je ve!kost stran trojuholnika ABC tato:

V

C

£

B

Obr. 110

AB = a, AG = c₂1, BG = t.

Ak chceme vytyći£ bod G (napr. kolikom), musime urcit yzdialenosf BG.

Plan riesenia. Najskór urcime veIkosf uhla BAO pomocou vztahu

sin<£ BAC =

c₂1

93