1954 Geometria 010

7. V trojuholnlku łeżia opróti zhodnym stranam zhodne vnutorne uhly, oproti va8§ej strane leżi vacśi vnutorny uhol. Możno tieto poucky obratit?

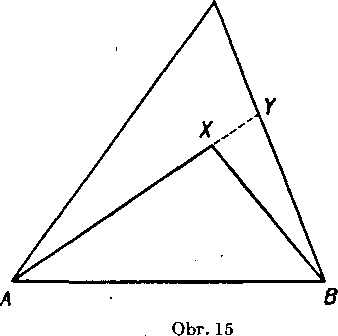
Obr. 16

8.    Vypocitajte vnutor-ne a vonkajśie uhly trojuholnika, akma vonkajśi uhol pri vrchole A ve!kosf 80° a vnutorny uhol pri vrchole B vel-kos< 48°.

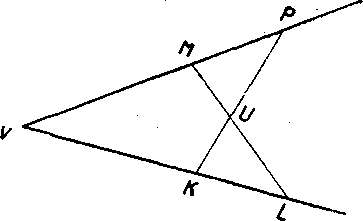
9.    Na obr. 16 je VM — « VK, VP = VL. Dokażte, że plati KU = MU, LU = =*Pi7.

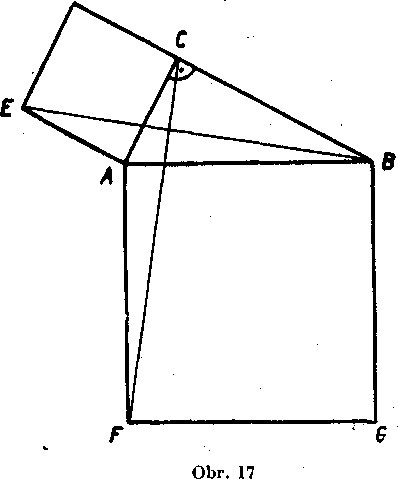
10.    Na obr. 17 je A ABC pravouhly, ACDE, ABGF su śtvorce. Dokażte, że

A A BE a, a ACF.

3. Zhodnosf ako premiestenie

Vratime sa teraz k poucke (5). Utvar, o ktorom sa v nej hovori, może byt tież rovina; premiestenie roviny si znazorńujeme pomocou prie-svitneho papiera, ako ste to robili v 7. roeniku. Premiestenie roviny yyjadrujeme aj slovom „zhodnosf”.

Zhodnosti _triedime do dvoch skupin; zhodnosti prveho druhu si nióżeme znazornit prostym pohybom priesyitneho papiera po podlożke a volame ich priame. Zhodnosti druheho druhu si znazorńujeme tak,

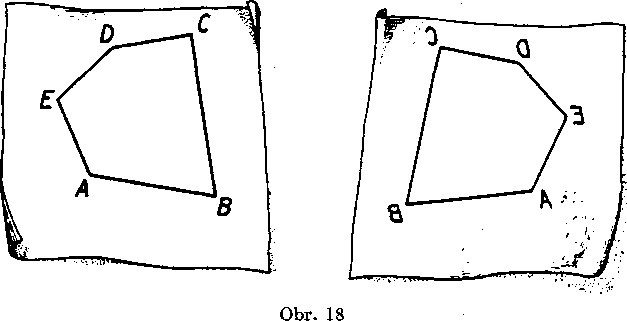
że priesvitny papier obratime najskór naruby a potom ho polożime IubovoIne na podlożku; tieto zhodnosti volame nepriame (obr. 18).

Poucka (5) nas vedie k tomu, aby sme sledovali premiestenie jednot-livych bodov roviny. Póvodny bod spravidla nazyvame vzor, pre-miesteny bod nazyvame jeho obraz. Osobitne si vślmame tie body roviay, które ostanu pri premiesteni na svojom mieste; tieto body Yolame samodruźne.

Z poućky (5) vyplyva bezprostredne reta:

(6) Ak pri premiesteni prejde niektóra polpriamka sama do seba, każdy jej bod je samodruźny.

Skutocne, ked prejde polpriamka A5 sama do seba, prejde bod A sam do seba; obraz X' jej bodu X dostaneme tak, że nanesieme useeku AX na polpriamku AB (obr. 19); je teda X' = X.

11