1954 Geometria 016

7.    Narysuj te Iuboyolny trojuholnik ABC a zostrojte jeho łazisko T. Zostrojte trojuholnik A'B'C', który rznikne z trojuhołnika ABC posunutim, które prevadza bod A do bodu T.

8.    Narysuj te pravouhly lichobeżnlk ABCD so zakladńou AB a pravym uhlom <X B. Zostrojte lichobeżnlk A'B'C'D' sumerne zdrużeny s lichobeżnlkom ABCD podia stredu A. Lichobeżnlk A'B'C'D' posunte tak, aby bod D' preśiel do bodu A'.

4. Krużnica. Obvodovy uhol

V 8. rocnlku sme preberali niektóre zakladne ylastnosti krużnice. Poznali sme, że krużnica je sumerna podia svojho stredu a podia każdej priamky, która prechadza stredom. To znamena, że krużnica prejde sama do seba sumernostou podia svojho stredu i sumernostou podia każdej priamky, która prechadza stredom.

Body roviny sme roz-triedili vzhl’adom na danu krużnicu do troch Skupin: prvu skupinu tvoria body krużnice, druhasku-pina su body vo vnutri krużnice, t. j. body, których vzdialenost od stredu krużnice je menśia neż polomer, a tretia skupina su body zvonku krużnice, t. j. body, których vzdia-lenost od stredu krużnice je vacśia neż polomer.

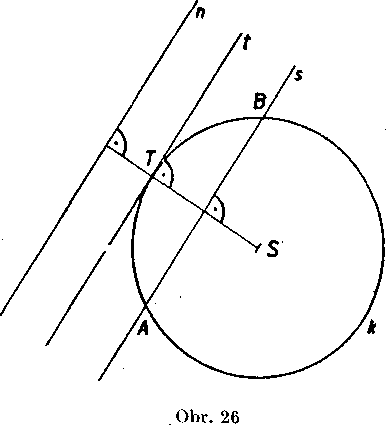
Skutnat vzajomnu po-lohu priamky a krużnice znamena zistit, akeho druhu vzhIadom na danu krużnicu su body danej priamky. Poznali sme, że su możne tri pripady: alebo vśetky body priamky leżia zvonku krużnice a priamka sa vola nesecria (n na obr. 26); alebo jediny bod T priamky leżi na krużnici a ostatne leżia zvonku krużnice, priamka je dotyćnicou krużnice [t na obr. 26); alebo ma priamka s krużnicou, spolocne dva body A, B; body leżiace medzi bodmi 4, B su vo vnutri

krużnice, ostatne body priamky Ali su zvonku krużnice. Takato priamka sa vola secna (s na obr. 26). Jednotlive pripady yzajomnej polohy priamky a krużnice rozliśime podia vzdiaIenosti d danej priamky od stredu krużnice. Ak je priamka nesecna, je d > r (r znaci polomer krużnice), ak je dotycnica, je d = r, ak je secna, je d < r. Tieto tri poućky możno obratif .

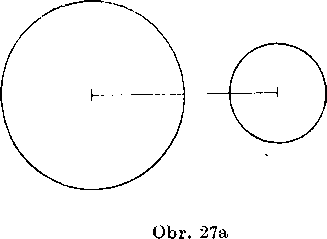
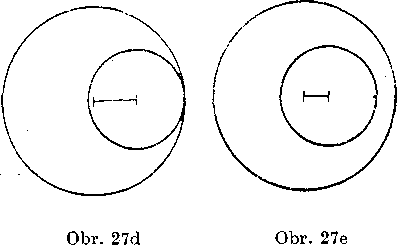
Pri skumani yzajomnej polohy dvoch nesustrednych krużnic s różnymi polomermi sme zistili, że je możnych celkom 5 pripadov: krużnice alebo leżia mimo seba (obr. 27a), alebo maju vonkaj§i dotyk (obr. 27b), alebo sa pretinaju vo dvoch bodoch (obr. 27c), alebo maju vnutorny dotyk (obr. 27d), alebo jedna leżi vo ynutri druhej (obr. 27e).

Jednotliye pripady rozliśime podia vztahov medzi polomermi obi-dvoch krużnic a ich strednou. Ak oznacime r₁ > r₂ obidva polomery, s strednu, platia vety: Ak leżia obidve krużnice mimo seba, je $ > r₁ Ą-+ r₂, ak maju vonkajśi dotyk, je s = r_x -j- r₂, ak sa pretinaju, je r_x — — r₂ < s < r_x A r₂, ak maju ynutorny dotyk, je s = r_x — r₂ a napokon ak leżi druha krużnica vo ynutri prvej, je s < r_x — r₂.

Tychto pat pouciek móżeme aj obratit.

17